チェビシェフの不等式は、下記の式です。
確率変数X、平均μ、標準偏差σがあった時の、確率がkという数字で求まってしまうことを表しています。
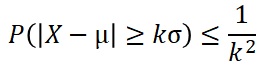
例えば、平均が０、標準偏差が１の時、-2から2の範囲よりも外になる確率は、 左辺のkが２の時を表すので、それを右辺に入れて計算すると、「0.25よりも小さい」という事がわかります。
チェビシェフの不等式の面白いところは、「どんな分布でも成り立つ」というところです。 精度が低い推定値なのですが、「少なくとも、この値よりも小さい」ということは計算できます。
チェビシェフの不等式は、「どんな分布でも成り立つ」と「精度が低い」というところが特徴です。 そこで、「どんな分布でも成り立つ」というのは、どういうことかということと、どれくらい精度が低いのかを検証してみました。
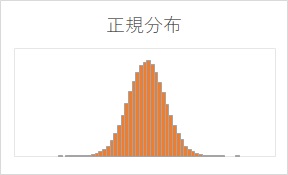
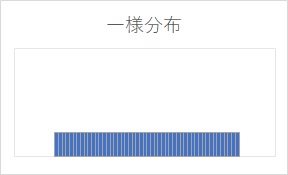
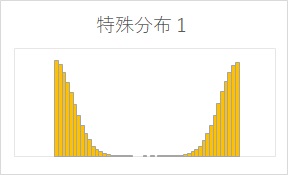
検証したのは、３種類の分布です。 正規分布と一様分布がわかれば、一般的に知られている分布がだいたいどんな感じになるのかが推測できるので、まず、この２つを選びました。 特殊分布1というのは、正規分布を真ん中で２つに割って、ずらすことで作った分布です。 正規分布と、一様分布は解析的に正確な値が求まるので、その計算をしています。 特殊分布１は、10万個の乱数データを作って、数えました。
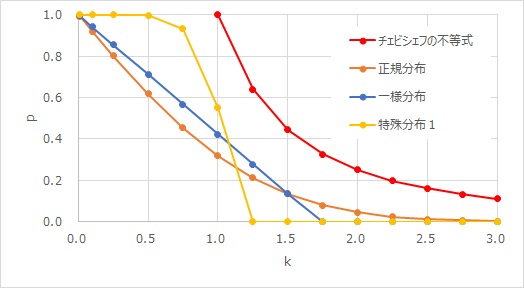
まず、わかるのは、kが１よりも小さいと、確率が１よりも大きく計算されるので、チェビシェフの不等式はまったく役に立たない点です。
kが2の時は、一様分布や特殊分布１は、確率が０になります。 チェビシェフの不等式の不等式だと0.25になり、正規分布の約５倍あります。
標準正規分布 の場合に、k＝１、２、３の時に、確率がいくつになるのかは、実務でもよく使われます。１σ、２σ、３σ、などとも呼ばれています。 正規分布に何となく近い分布なら、良い目安になります。 １σが0.3（30%）、２σが0.05（5%）、３σが0.003（0.3%）です。
チェビシェフの不等式と直接の関係はないのですが、上記の検証によって、一様分布や特殊分布１のように、両端に絶壁があるような分布だと、 k＝２あたりでは、０になっていることがわかります。 正規分布とは全然違うような分布の時に、これは目安になります。
「行動計量学序説」 林知己夫 著 朝倉書店 1993
多次元のチェビシェフの不等式が紹介されています。
また、チェビシェフの不等式の精度を上げるための計算方法が、２種類紹介されています。
１つはモーメントを考慮するもので、大きめに計算される値を直接的に小さく計算する方法になっています。
モーメントをいくつかにするのかが、合わせ込みのような作業になり、実用的ではないように見受けられました。
もう１つは、サンプル数が少ない時に、正確に計算される方法になっています。
こちらは、式が複雑になり、kとσの関係がわかりにくいので、実用的ではないように見受けられました。
「直感的統計学」 吉田耕作 著 日経BP社 2006
確率の計算方法のガイドがあります。
・nが30以上の時は、中心極限定理が成り立つので、正規分布と仮定して確率を計算
・nが30未満の時で、正規分布が仮定できる時は、正規分布かt分布で計算
・nが30未満で、非正規分布の時は、チェビシェフの不等式で計算
「統計学」 中村和幸 著 東京図書 2017
大数の法則の導出に、チェビシェフの不等式が使われています。
順路
次は
比例分散
