矢印が因果関係の場合と、因果関係ではない場合

以下は、筆者の私見です。誤解があれば、ご教示いただけると幸いです。

統計的因果推論では、「有向グラフ」と呼ばれている、矢印を使った図が出て来ます。この矢印について、「因果関係を表している」と説明されることがあるのですが、間違っていることがあります。

このページでは、どんな時に因果関係を表していて、どんな時にそうではないのかを整理しています。

矢印が因果関係の場合

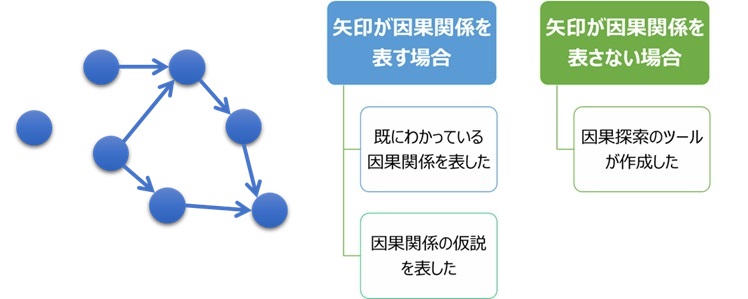
矢印が因果関係を表している場合は、３つあります。

例えば、料理なら、材料の量や品質、調理方法、等が原因で、味や見た目が結果なことは、わかっているので、因果関係を矢印で表すことができます。

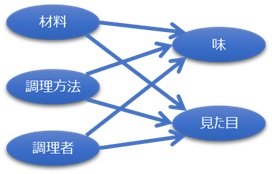
矢印が因果関係の場合と、因果関係ではない場合

製造プロセスや、化学現象などでも、同じように矢印を使った図を使えます。

「因果関係はこうではないか？」と、仮説を表現したい時に、矢印を使った図は便利です。

例えば、故障が起きた時に、原因や原因同士の因果関係について、考察したのが下の図です。
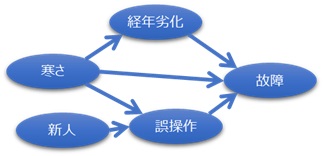
矢印が因果関係の場合と、因果関係ではない場合

この図は、あくまで仮説なので、この後に、どれが本当なのかや、抜けていることがないのかを確認する必要があります。

この図が、「既にわかっている因果関係を表した」と、「因果関係の仮説を表した」のいずれなのかは、当事者以外は区別できないことがあるので、人に見せる場合は、説明の仕方に注意が必要です。なお、書いた本人が、混同していることもあるので、説明される側の人も、注意して聞いた方が良いです。

因果推論の専門家は、まず、「因果関係が成り立っていれば、データの構造はこうなる」と、因果関係を定義します。

実際のデータを調べて、定義を当てはめれば、矢印の向きが決まります。

有向グラフを作る方法は、「因果探索」と呼ばれています。因果探索のツールは、自動的に分析して、有向グラフを出力します。

有向グラフを見ると、それが何を表しているのかに関わらず、「因果関係を表す図だ」や、「因果関係の仮説を表す図だ」と思う人が少なくないようです。

しかし、以下の２つの理由があるので、矢印は因果関係を表していないです。

因果探索のツールは、何らかの因果関係の定義に基づいて、有向グラフを作ります。

知りたい因果関係がその定義に合っていれば良いのですが、合わないことが普通です。

因果探索は、３つ以上の変数の間にある、複数の因果関係について調べる方法として使います。その内のいくつかについては、定義に当てはまったとしても、当てはまらないところも出て来ます。そのため、全体としては、合わないことが普通になって来ます。

因果推論の文献は、専門家の立場で書かれることが多いです。専門家の立場では、定義に合っていれば、因果関係を見つけられたことになります。そのため、「因果探索で見つけた有向グラフは、因果関係を表す」となります。

一方、実務家の立場では、「因果関係のメカニズムがどうなっているのか」、「そのメカニズムは、データに表れているのか」、「データに表れているのなら、どのようにして表れれているのか」という点が、合って来ないと「因果関係がデータからわかった」とはなりません。
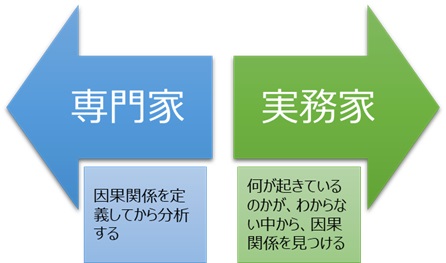
矢印が因果関係の場合と、因果関係ではない場合

上記では、説明が煩雑になることを避けるため、「因果探索のツールは、定義に合う因果関係を見つける方法」として説明して来ました。

ところが、実際は、定義に合う因果関係を見つけるのは、そんなに簡単なことではないです。因果探索は、非常に多くの組合せがある中から、もっともらしい答えを見つけることになるのですが、それに加えてデータ自体が持っている偏りも影響して来るので、定義に合う因果関係が、うまく見つからないことがあります。