トップページ |
統計学の解釈学 |
このサイトについて
トップページ |
統計学の解釈学 |
このサイトについて
以下は、筆者の私見です。 誤解があれば、ご教示いただけると幸いです。
統計的仮説検定 は、統計学に詳しい人でも、使い方が不十分で失敗することがあります。
よく起きる失敗を、段階別に説明します。
まず、検定を知らないと起きる失敗です。
下の表は、不良品の対策を考え、対策なしと、対策ありで、１週間実施した結果です。
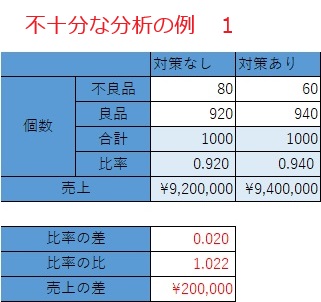
合計が同じです。対策ありの良品の方が、20個多いです。 この商品は、１個10000円するので、対策ありの方が、20万円高いことになります。
この結果を見ると、「10000個作れば200万円、100000個作れば2000万円、売上が上がる！」となります。
ところが、このくらいの比率の違いは誤差の範囲のため、実際は対策の効果がなく、何も変わらないことがあります。
次に、検定を知っていても起きる失敗です。
検定を知っている人は、上記のような考察の仕方が不十分だと知っています。 「比率の差が0.02（2%)や、比率の比が1.022倍なのは、誤差の範囲かもしれない。 もしかしたら、対策に効果がないかもしれない。」と考えます。
上記について、検定の結果を加えると、以下になります。
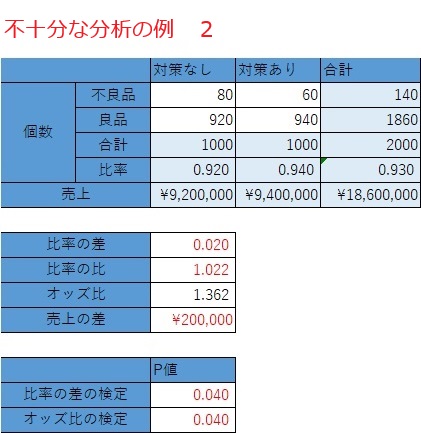
比率の差の検定でも、オッズ比の検定でも、P値が0.05以下です。 そこで、「検定でも、対策に効果があることが確認できた！」となります。
ところが、ここまで確認して、対策案をスタートさせたのに、その後、対策前と同じくらいだったり、対策前よりも悪化することがあります。
なお、この進め方は、統計学の検定としては、正しいです。 しかし、実務の中でのデータ分析としては、不十分です。 それが失敗の原因です。
対策なしと、対策ありで、比率の差が0.02あり、1000個ずつ作ってみたら、20万円の差が出たことは正しいです。
上記の分析で失敗する原因は、「未来についても、同じくらいの差になる」と、暗黙の前提を置いているところにあります。 別の言い方をすると、「真の比率があって、未来になっても一定」という、前提を置いています。
このページで「見えない誤差」と呼んでいるのは、過去から未来にわたっての、真の比率の変化の仕方です。
「1000個も確認した」、「P値が十分に小さいことを確認した」、「金額が十分に大きいことを確認した」というように思っていると、失敗しやすいです。
差の意味で検定を補強 のページに「経済的に意味のある差」についての説明があります。 比率の差や、比率の比を見ても、意味のある違いかどうかがわからない時は、経済的な意味を考えると良いのですが、 この例の場合、「20万円」というのが落とし穴になります。
「20万円」というのは、日常生活で使う金額としては、大きいです。そのため、「大きい」という感覚になりやすいです。 しかし、この商品の売上全体で見ると、20万円は誤差の可能性があります。 「20万円が誤差」ということに気付きにくいです。
差の意味で検定を補強 のページには、「よく起きている差」についての説明もあります。
例えば、対策実施前の１週間ごとの推移が、以下のようになっていたとします。
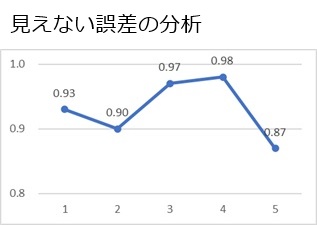
低い時は0.87、高い時は0.98です。 これが通常なら、対策ありの0.94という数字が、普段の比率の範囲なのか、対策の効果なのかは、区別がつかないです。
「未来についても、同じくらいの差になる」ということの確認はできませんが、過去を確認することはできます。
上記の例では、過去のデータがありましたが、「新しく始める事業について、A案とB案を試験的にスタートして結果を比較」といった場合は、過去のデータはないです。
過去のデータがない場合でも、似た事業の過去のデータなどから、比率がどのくらいの範囲で推移するのかを見積もっておくと良いです。 そうすれば、A案とB案の比率の差が、見えない誤差と比べた場合に、どの程度なのかが判断できるようになります。
「過去のデータも分析に含めた方が良い」ということで、過去のデータを全部まとめて、対策ありのデータと検定をするのは間違ったやり方です。 「真の比率は一定のはずだから、それを正確に出すには、過去のデータを全部使えば良い」という進め方になってしまっています。 そのように進めてしまうと、普段の比率のばらつきがわからないです。
また、比率の信頼区間は、普段の比率のばらつきではないです。
