トップページ |
統計学の解釈学 |
このサイトについて
トップページ |
統計学の解釈学 |
このサイトについて
以下は、筆者の私見です。 誤解があれば、ご教示いただけると幸いです。
時系列近傍法 では、定常性がデータを見るポイントのひとつになっています。
「定常」というのは、時間が経過してデータが増えても、平均や分散（標準偏差）は、ほとんど変わらないことをいいます。
例えば、下は定常な場合の例です。
増減があるものの、平均が約100なのは変わらないように見えますし、全体的なばらつきの範囲も変わらないように見えます。
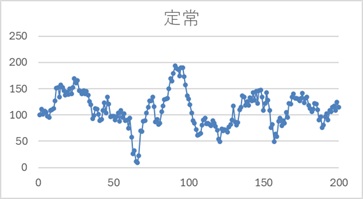
次に、下は非定常な場合の例です。
上がっていく一方なので、平均も分散も大きくなる一方です。そのため、「非定常」ということになります。
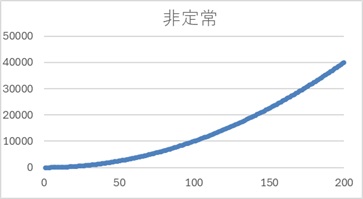
定常性の条件が知られていて、特に、AR(1)とAR(2)の場合は、わかりやすい条件になっています。
上記の、定常・非定常の例について、AR(1)とAR(2)の時の係数、a1、a2を見ると、確かに上の条件に合っています。
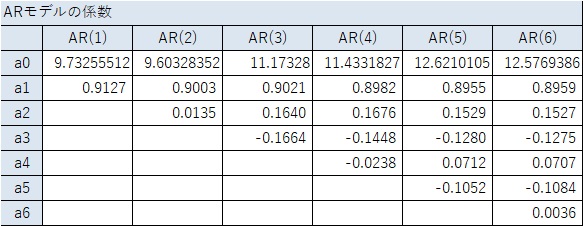
ところで、下の例は、平均も分散も大きくなる一方のようなので、「非定常」のように見えます。
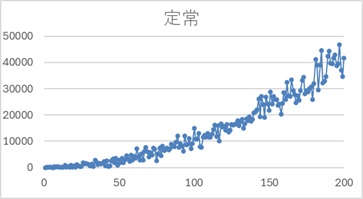
ところが、定常性の条件を確認すると、この例は「定常」ということになります。
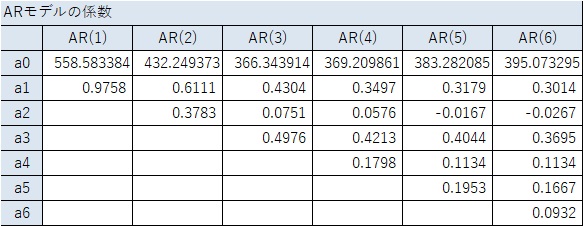
非定常に見えるデータでも、「定常」と判定される理由として、以下の２つがあるようです。
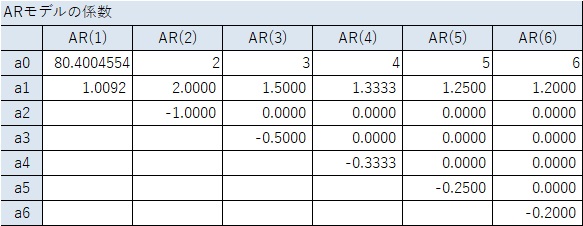
例えば、下の例は、「a1 = 2、a2 = -1」となっているモデルで作ったデータです。
この係数なら、非定常になるはずです。
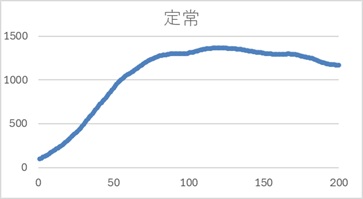
ところが、実際に係数を計算すると、下表のようになり、条件と照らし合わせると、「定常」ということになります。
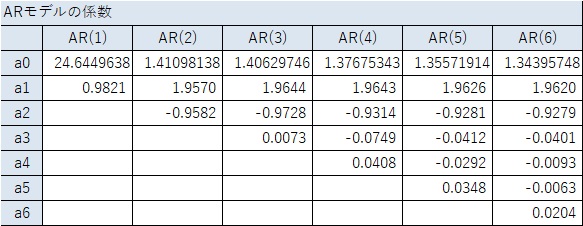
この理由として、モデルの式は「非定常」の条件でも、乱数を使って作ったデータなので、実際のデータは非定常になっていないことが考えられます。
「a1 = 2、a2 = -1」となっているモデルで作ったデータが良い例ですが、非定常になるように係数を決めて作ったデータは、「隣接した値がとても近い」ということが、必ず成り立つようです。 理由が不明ですが、筆者の経験の範囲では、「必ず」になっています。
非定常に見えるけれども、定常なモデルの例のデータは、ベースになる曲線から、毎回ばらついたようなデータになっていて、隣接した値は、それほど近くありません。
定常性の条件は、ARモデルで作られたデータに対して導出されているようです。 任意の時系列データに対して、ARモデルを適用して係数を求めることはできますが、条件の導出時に想定外の状態をデータが持っているために、定常性が正しく判断できないのではないかと筆者は考えています。
