反実仮想による因果効果の分析 のRによる実施例です。
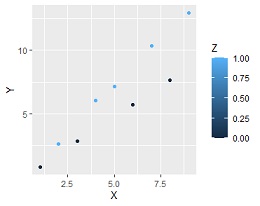
目的変数はYです。 処置あり1、処置なし0の変数はZという名前です。
下記の実施例では、Xという変数が１つある場合ですが、
モデルは、Xが複数あっても作れます。
「X」という変数がないとエラーになるのは、散布図を作る行です。
反実仮想を求めるためのモデルは、 一般化線形モデル を入れています。 この部分を変えると、いろいろなモデルが使えます。
T-Lerner なので、モデルが２つ作られます。
library(ggplot2) # ライブラリを読み込み
setwd("C:/Rtest") # 作業用ディレクトリを変更
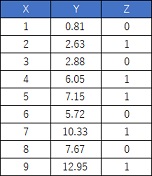
Data <- read.csv("Data.csv", header=T) # データを読み込み
DataZ <- Data
Data0 <- subset(Data, Data$Z == 0)# Zが0のサンプルのデータを別に作る
Data1 <- subset(Data, Data$Z == 1)# Zが1のサンプルのデータを別に作る
DataZ$Z <- NULL # Zの列を消す
Data0$Z <- NULL # Zの列を消す
Data1$Z <- NULL # Zの列を消す
gm0 <- step(glm(Y~., data=Data0, family= gaussian(link = "identity"))) # Z=0の一般化線形モデル
predictedY <- predict(gm0,Data0)#
Data01 <- cbind(Data0,predictedY)#
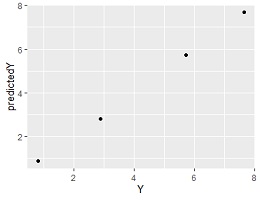
ggplot(Data01, aes(x=Y, y=predictedY)) + geom_point()# Z=0の予測値と実測値の関係の確認
gm1 <- step(glm(Y~., data=Data1, family= gaussian(link = "identity"))) # Z=1の一般化線形モデル
predictedY <- predict(gm1,Data1)#
Data10 <- cbind(Data1,predictedY)#
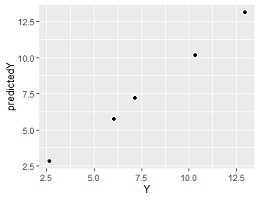
ggplot(Data10, aes(x=Y, y=predictedY)) + geom_point()# Z=1の予測値と実測値の関係の確認
s0 <- predict(gm0,DataZ)#
s1 <- predict(gm1,DataZ)#
causal_effect <- s1-s0# 因果効果を計算
DataS <- cbind(Data,s0,s1,causal_effect)#
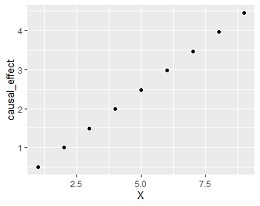
ggplot(DataS, aes(x=X, y=causal_effect)) + geom_point()# Xと因果効果の関係
ggplot(DataS, aes(x=X, y=Y)) + geom_point(aes(colour=Z, shape=Z))# 元のデータのグラフを作る
