Excelによるデータ分析
Excelによるデータ分析
曲線近似による予測 では、予測値をグラフから読み取る必要があります。
任意の場合の予測値を計算したい場合は、以下のようにして、関数で計算する方法があります。
線形近似 は、 単回帰分析 による予測です。 説明変数が１個の時に使います。
以下の方法は、説明変数が２個以上あり、 重回帰分析 をしたい場合にも使えます。
まず、データを用意します。
予測したいのは売上です。
「データ」タブの、「データ分析」を選びます。
「回帰分析」を選びます。
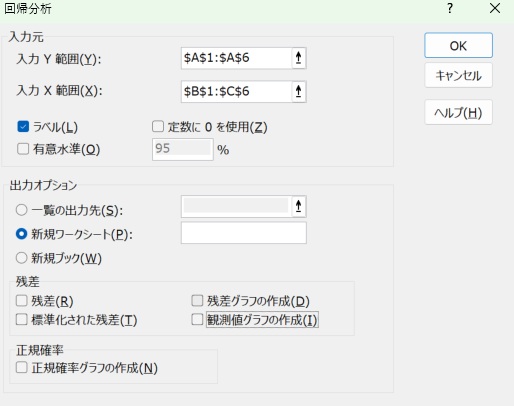
データの範囲を入力します。
Yが元データで、Xが新しく作った変数です。
ラベルにもチェックを入れます。
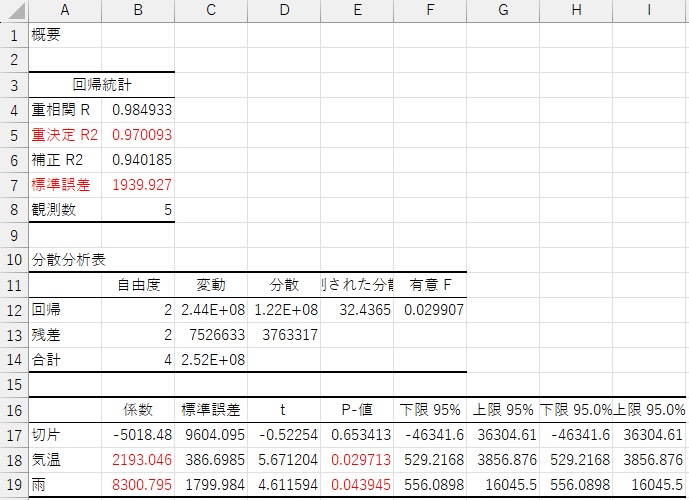
分析データが新しくできたシートに記入されます。
まず、重決定R2（相関係数Rの二乗：寄与率）が0.97…なので、高い精度があることがわかります。
精度については、標準誤差からもわかります。 予測区間 は、標準誤差の±約２倍の範囲が95％の予測区間になります。 標準誤差が約2000（1929…）となので、予測値を中心として、上下に約4000円ずつばらつきがあります。 そのため、これは、例えば、「予測値が50000円の場合、実際は46000円〜54000円にある可能性はあるが、その範囲より外は可能性が低い」ということがわかります。
気温の係数が約2000（2193…）ですが、これは、1℃上がると売上が約2000円上がることを意味しています。
雨の係数が約8000（8300…）ですが、これは、雨の時の方が、売上が約8000円高いことを意味しています。
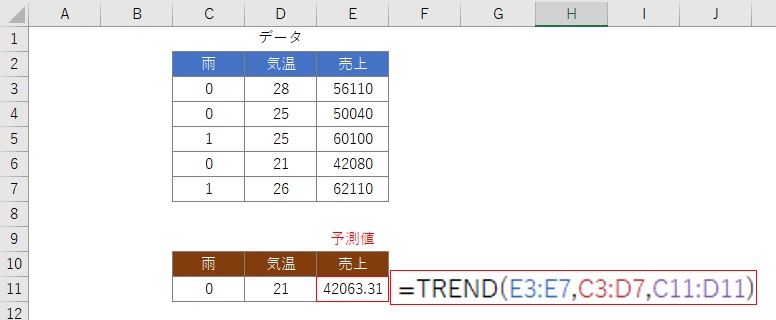
TREND関数を使うと、 重回帰分析 による予測ができます。
下の例は、30℃で雨の時と、25℃で晴の時の予測です。
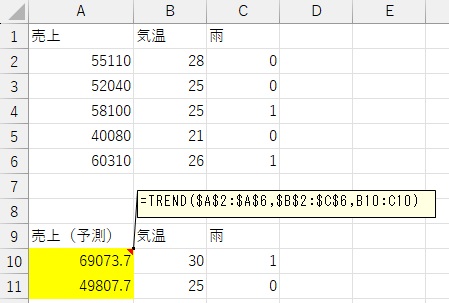
なお、データは、21℃から28℃なので、 外挿 です。 そのため、予測はできますが、取り扱い注意です。
25℃で雨の時のデータがあるので、25℃で晴の時は、「 反事実 」と言います。
TREND関数で予測できるのは、中心値です。 予測シートのように、予測区間は出ませんが、予測区間は、中心値に標準誤差から求めた予測区間を加味したものになります。
天気なら、データは「晴」、「雨」、「曇」としたいところですが、TREND関数は数値データしか扱えないので、 ここでは、「雨 ＝ １」としました。
０と１しかダメなわけではないので、「曇 ＝ 0.5」としたり、 「半日雨 ＝ 0.5」という工夫もできます。
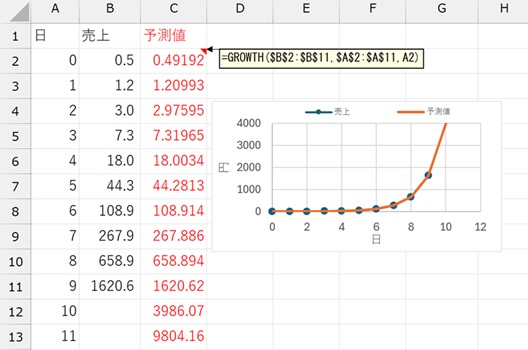
指数近似の場合は、以下のように、GROWTH関数を使います。
GROWTH関数の場合、売上が0円の場合が含まれていると、指数近似ができないため、エラーになります。
