 Excelによるデータ分析
Excelによるデータ分析
 Excelによるデータ分析
Excelによるデータ分析
Excelでは、散布図や折れ線グラフが、そのまま予測のツールに使えるようになっています。
まず、データのある範囲を選択します。
「挿入」タブの中の「散布図」を選ぶと、グラフができます。
グラフが選択された状態では、「グラフのデザイン」が表示されます。「グラフ要素追加」、「軸ラベル(A)」と進み、「第1横軸(H)」と「第1縦軸(V)」を選ぶと、軸ラベルが記入できるようになります。
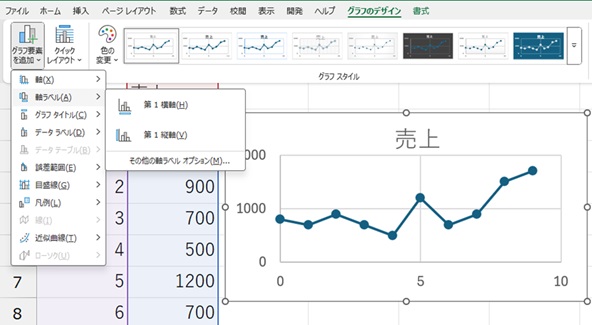
グラフのデザインを修正すると、例えば、次のグラフになります。
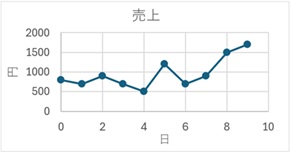
データを選んだ状態で、右クリックをします。「近似曲線の追加(R)」を選びます。
一番当てはまりの良い近似曲線を探します。チェックを変えると、描かれる曲線が変わるので、試行錯誤すると良いです。
参考として、それぞれの近似の特徴を説明します。
なお、移動平均は、近似曲線のオプションに含まれていますが、「近似曲線」という名前に合わない方法です。 また、移動平均だけ、予測ができるようになっていません。
指数近似は、急激な上昇がある時に適した曲線です。「指数関数的な上昇」という表現がありますが、その指数関数を使うのが、指数近似です。
Xと、Xの増加速度に比例関係があると、この曲線になります。例えば、化学反応で見ることがあります。
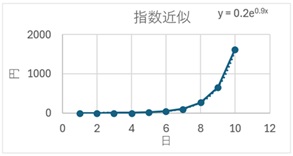
線形近似は、直線による近似です。全体的に上昇や下降のトレンド(傾向)がある時に適しています。
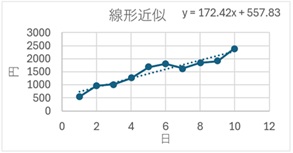
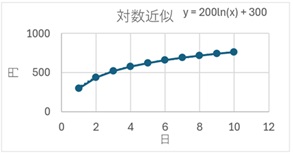
対数近似は、時間が経てば経つほど、上昇が緩やかになる曲線です
。
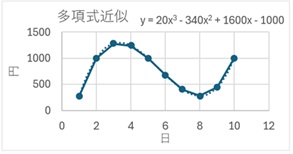
多項式近似は、カーブが多い時に適しています。下の例では、2回カーブする場合ですが、この時は「次数」を「3」にします。
なお、「次数」が「1」の場合は線形近似と同じになりますが、Excelでは「1」は指定できないようになっています。
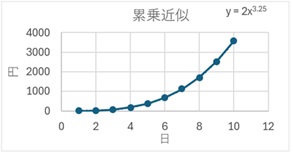
累乗近似は、指数近似よりも緩やかな曲線になります。
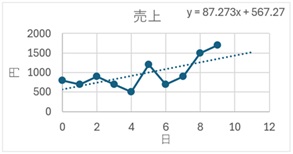
以下では、「線形近似(L)」で説明します。 「前方補外(F)」を「2.0」にします。「グラフに数式を表示する(E)」にチェックを入れます。
すると、グラフに予測値を表す直線と、その直線の数式が記入されます。前方補外を「2.0」にしているので、予測値は2日後まで計算されています。
近似曲線で、簡単に出せるのは中心値だけです。 また、近似曲線の選択肢の中には、周期的な変化を扱えるモデルがないです。 そのため、 予測シート よりも不便です。
しかし、近似曲線には予測シートにはない利点があります。
1つめの利点は、簡単な数式が得られるところです。
この数式の使い道ですが、例えば、この例で使っている線形近似の場合、数式の中にある「87.273」という数字は、1日あたりの売上の増加量を表しています。
2つめの利点は、予測できる範囲が長い事です。
予測シートでは、新しいデータほど重要視して予測します。 そのため、数日後や、1周期後くらいの範囲については良いのですが、それよりも後については、予測のもっともらしさがあまりないです。
近似曲線では、データの新しさとは無関係に、データ全体について、当てはまりの良い曲線を検討します。そのため、当てはまりの良い曲線が得られれば、比較的長い範囲について、その曲線を前提にした予測をしても、大きく外れにくいです。
3つめの利点は、「データが等間隔」という条件がないことです。
近似曲線の場合、任意の時刻に測定したデータでも扱えます。
このページの分析を実際にやってみる時に、混乱しやすいことがあります。
上記では、時刻を表すA列を、0から始まる日数にしています。 日付にはしていないです。
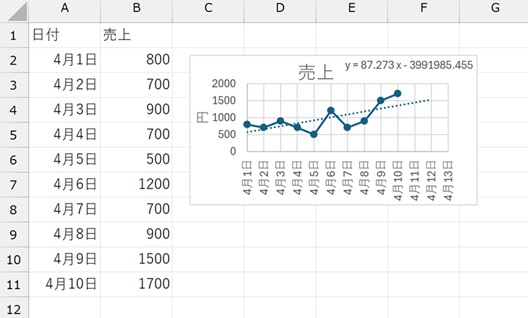
日付で分析をすると、下のようになります。 作られた数式を見ると、「87.273」部分は同じですが、もうひとつの数字が「-3991985.455」という数字になっているところが違っています。
Excelでは、1900年1月1日を「1」として、そこからの日数で日付のデータを処理しています。 2025年4月1日は、「45748」です。 ちなみに、この日の午前6時は、45748.25です。 「45748.25」と入力して、書式を時刻に変更すると、「2025/4/1 6:00:00」になります。
近似曲線は、日付を数字に変換してから求められています。そのため、この例の場合は、「-3991985.455」という値が計算されています。
近似曲線の場合は、作られた数式をさらに利用することや、数式の考察を進めることがありますが、その時に、大きな値が含まれていると、計算ミスの原因になります。 そのため、時系列を表す変数は、経過時間にした方が良いです。

