クラスターの予測の分析 では、「どのクラスターに属しているのか？」が、わかります。
分析の目的によっては、「どのクラスターにも属していないのでは？」という、外れ値かどうかの判断をしたいことがあります。 しかし、クラスターの予測の方法では、必ずどこかのクラスターに振り分けるので、これはわかりません。
「どのクラスターにも属していないのでは？」は、それぞれのクラスターに対して、「このクラスターには属しているか？」を調べて行き、 その結果を集めるとできるようになります。 1クラスモデル の中間処理として、クラスター分析を使う方法になります。
「分析」や「層別」という言葉の説明の中で、 「分ければ、分かる」という表現が使われますが、クラスター分析を使った外れ値の予測も、「分ければ、分かる」という方法になっています。 「分ける」を簡単に進める方法として、クラスター分析が役に立っています。
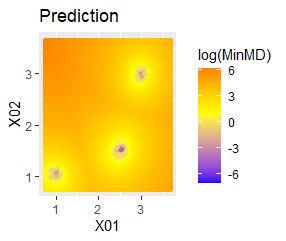
混合分布法ではなく、混合分布MT法を使って、例えば、任意の位置のクラスターを予測すると、下図になります。
各クラスターの中心から遠いほど、値が高くなっていて、外れ方の大きさがわかります。
「〇〇以上なら、どのクラスターにも属していないと考える」といった使い方ができます。
クラスター分析の手法のバリエーションと、判定方法のバリエーションがあります。
クラスター分析の手法のバリエーションとしては、k-Means法や混合分布法があります。 DBDCANなどでもできるかもしれませんが、複雑な形状の分布を扱えても、その後の判定方法に良さそうなものがなさそうです。
クラスター分析に、k-Means法や混合分布法を使うと、判定方法は、個々のクラスターの中心から、ユークリッド距離やマハラノビス距離などで見る方法が使えます。
混合分布MT法 は、外れ値の予測に使う方法の一種です。 クラスター分析の手法は混合分布法にして、判定方法は MT法 を使っています。
クラスター分析を使った外れ値の予測の方法と、 クラスター分析による外れ値の検出 は、違いがわかりにくいかもしれません。
サンプルがたくさんあって、「いくつかのクラスターと、外れ値のクラスターに分けたい」という時は、 クラスター分析による外れ値の検出 のページの方法になります。
クラスター分析を使った外れ値の予測の方法は、 「元になるデータがあって、これとは別のデータが元になるデータに入るかどうかを見たい」という時の方法になります。
Rによる混合分布MT法は、 Rによる混合分布MT法 のページにあります。
「機械学習のための特徴量エンジニアリング」 Alice Zheng・Amanda Casari 著 オライリー・ジャパン 2019
この本では、k-means法とロジスティック回帰分析を組み合わせることで、複雑な分布になっているラベル分類をシンプルに解く方法として紹介しています。
このページの「ベクトル量子化平均法」という方法は、この本を読んだ後で、「ロジスティック回帰分析を使わずに、もっとシンプルにできる」ということに
筆者が気付いてまとめたものです。
探せば、世の中に同じ方法があるかもしれないです。
順路
次は
ベクトル量子化平均法
