There are various algorithms for Structure Analysis by Bayesian Network .
This page is for investigating which algorithm is better when the purpose is the analysis of "examining the structure of data".
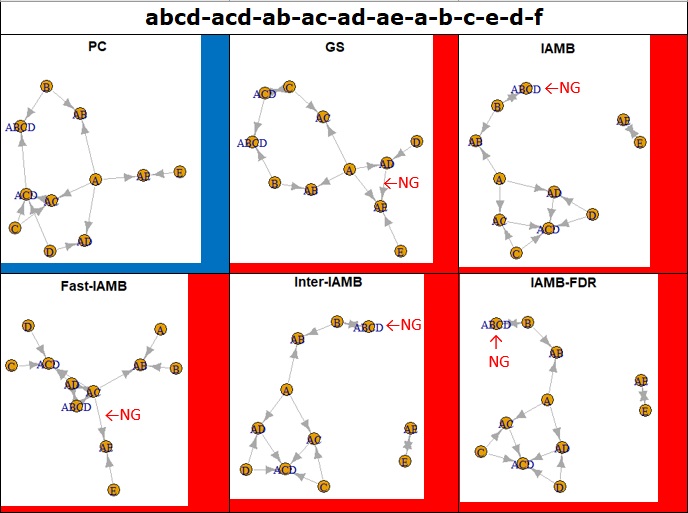
First of all, the conclusion is "The best algorithm is PC. "
The study also confirms that no matter which algorithm is used, quantitative variables should be converted to qualitative variables before analysis.
The number of samples is set to 10000 so that correct results cannot be obtained because there are not enough samples.
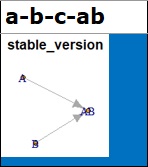
For example, in a table, the column "a-b-c-ab" is a qualitative variable for a table whose variables are A, B, C, and AB in order from the left.
"a-b-c-ab" and "ab-a-b-c" differ only in the arrangement of variables. This study also looks at the differences in how variables are arranged.
If the cell is blue, the graph is the same as the true structure. In this example, since AB is made with A and B, the correct answer is that there is an arrow from A or AB, B to AB, and C is not connected to anything, but that is true.

If the cell is black, you've got a result that you definitely don't want. In this example, A and B are independent, so the correct answer is not to connect them, but they are.
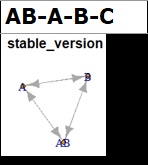
If the cell is red, the mistakes are the same as black. In this example, for example, A is not made from AC, but there is an arrow from AC to A.
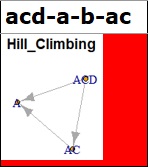
If the cell is green, you can't figure out the background of the data, but you'll be able to think about it to some extent. If the direction of the arrow cannot be determined only by the data, it is helpful if the arrow is not determined by just connecting it, because it will not be mistaken in the later analysis. In the case of the data in the red example above, this green-like graph is ideal for analysis.
The algorithm uses the R bnlearn and BNSL packages. I'm using the code, Bayesian Network by R.
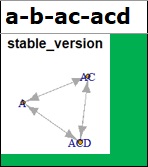
It is blue or green except for AB-A-B-C, which uses quantitative variables. This group is the best, so it's the conclusion at the beginning of this page.
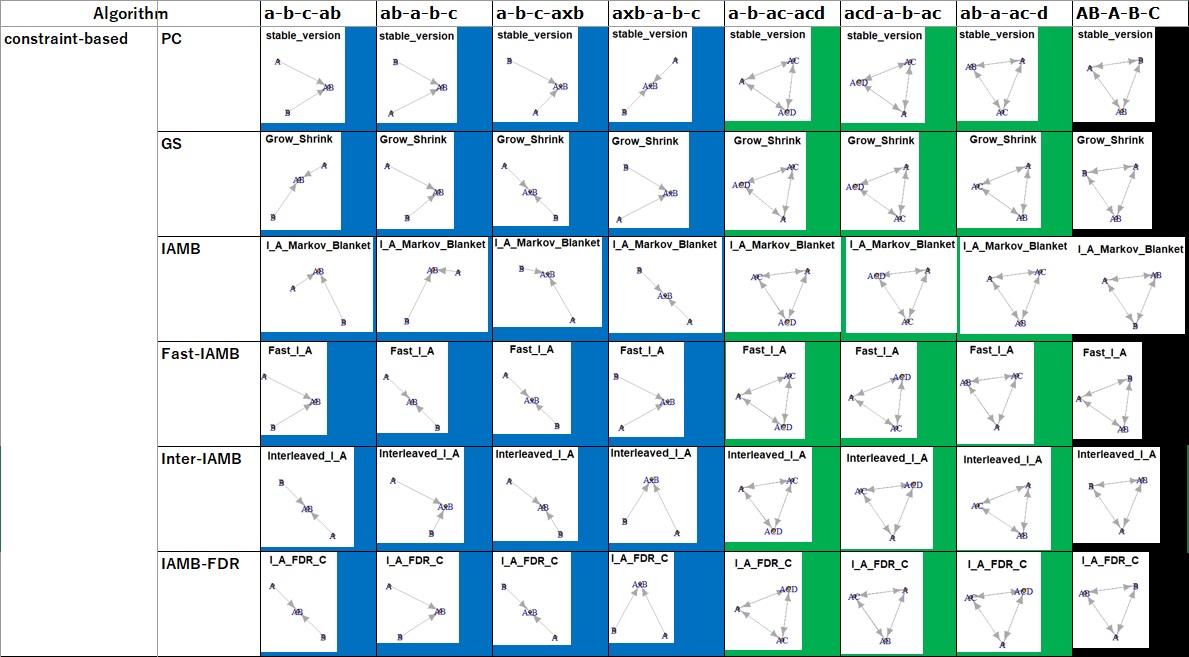
What can be made blue with the constraint-based (1) is green.
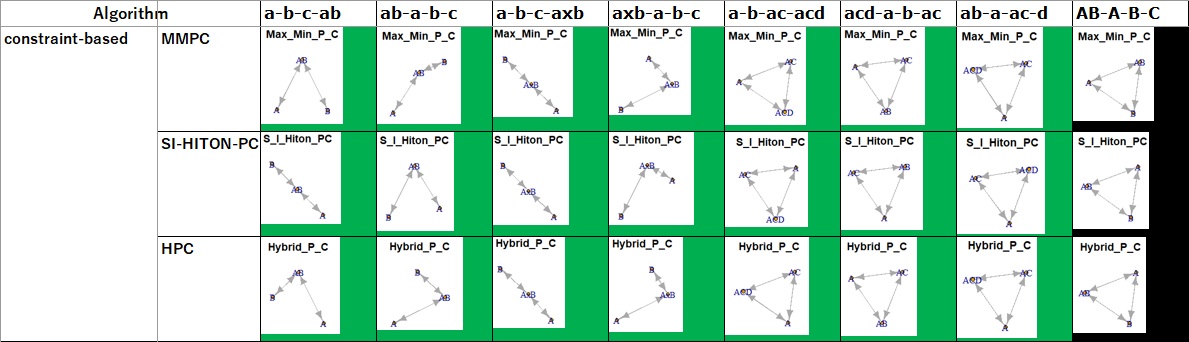
It can be blue or red just by changing the order of the variables. This feature may be used, but it is an unsuitable algorithm for analyzing data where you do not know if the order of the data makes sense.
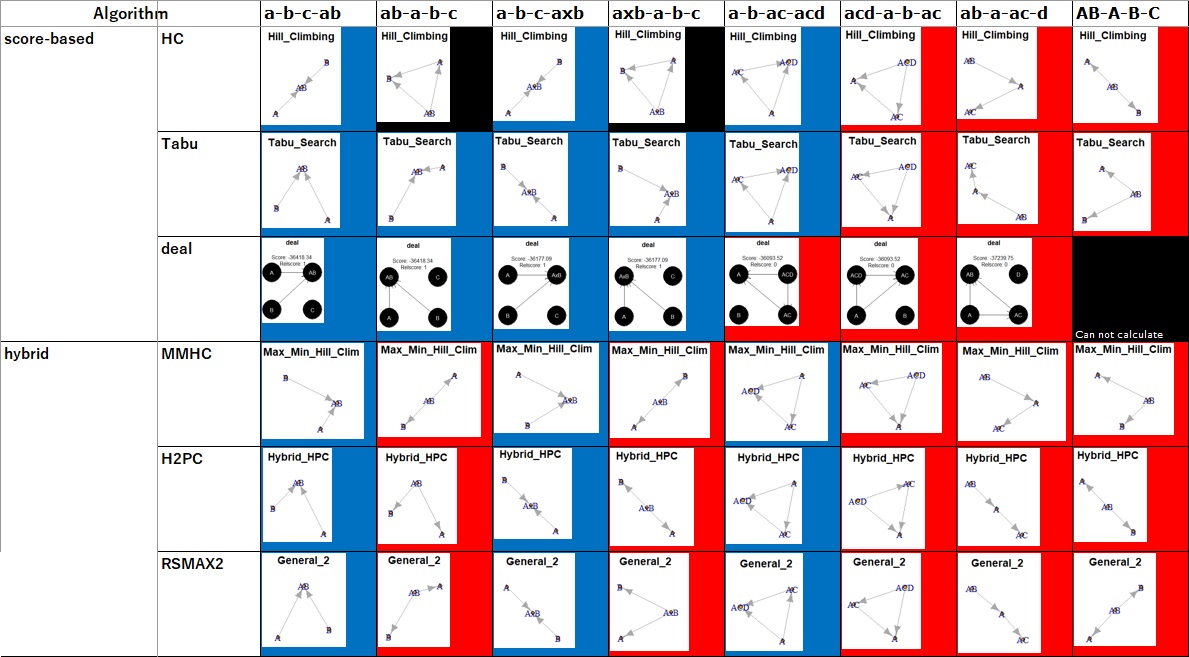
Since there is a lot of black, it cannot be used with this usage.
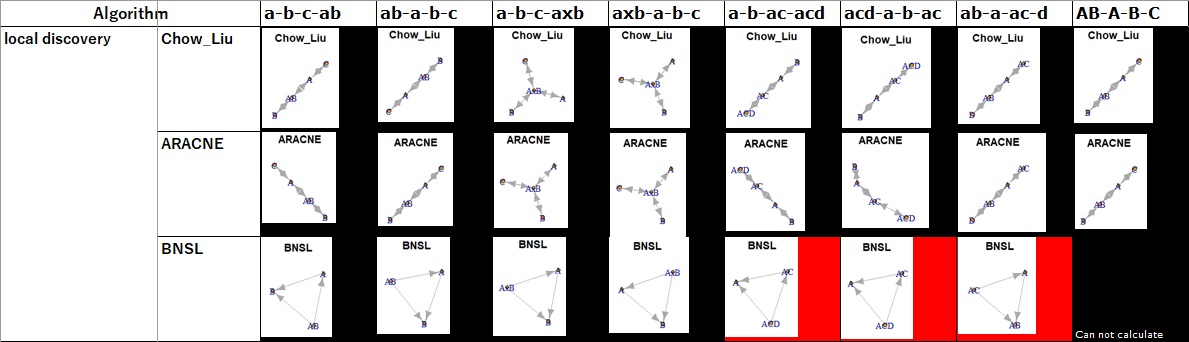
In the algorithm comparison (1), I found that the conditional-based group is good, but I don't see any difference in this group.
When I tried it with a little more complicated data, I found that the best one was a PC. Others were tied where they didn't want them to be tied, and the ABCDs they wanted the arrows to gather were isolated.
NEXT 

 Pattern Recognition by Bayesian Network
Pattern Recognition by Bayesian Network
