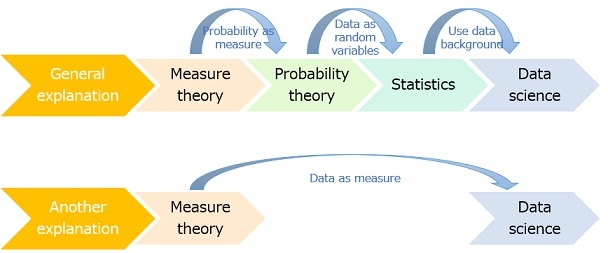
There are several books that explain measure theory as the basis of probability theory. Since probability theory is the foundation of statistics, measure theory is also the basis of statistics.
Measure theory and measure theory are widely supported and utilized in the academic world. In the academic world, it seems normal to talk about something that has already been completed. However, as an author, I feel that this is not the only thing in terms of actual data. This page also contains unorganized ideas. I think it is due to the author's lack of understanding or misunderstanding. This page is written with a policy of adding and correcting as necessary.
Measure theory is a branch of mathematics that literally describes "measure".
A measure is a type of thing that is routinely called a quantity. Among the so-called "quantities," those that can be added, such as length, area, and weight, seem to fit the definition of measure.
In measure theory, "What is a measure..." is not explained only in spoken language like in a dictionary, but in mathematical terms. If you can express it in mathematical terms, you will be able to conduct mathematical research on properties and characteristics.
"Set theory" is a field of mathematics that deals with the ideas of "overlapping and non-overlapping parts of two groups" and "whole and part".
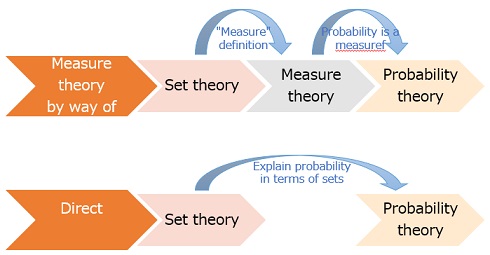
In measure theory, "measure" is defined using set theory.
In measure theory, when a measure is defined using set theory, it is defined as "measured" by dividing it into "measured object" and "measured object".
In order, first, the properties of things to be measured are defined using set theory. Next, we define the object to be measured correspondingly.
"It's common to use set theory to explain probability, but why use set theory to talk about length?" That was something I wasn't sure about.
What we get as length is the sum of the parts, and to express that "the whole is a collection of parts" and "there are no overlapping parts when adding up", The reason seems to be that the way set theory is written is just right.
n measure theory, it is common to describe lengths and areas among quantities. When we talk about probability theory, we think of "probability" as a type of quantity and deal with probability.
There are various quantities in the world, such as weight, brightness, etc., but the explanation of measure theory that deals with such various quantities I have never seen it.
As you can see on the Distinguishing and using data page, the amount that measure theory deals with is a part of what appears in data science called "quantitative data" or "quantitative variable".
From the standpoint of measure theory, probability is a type of measure. The measure that adds up to 1 is the definition of a measure called probability. Therefore, from the standpoint of measure theory, probability theory is a discipline that deals with the property of a measure called probability.
"It is common to use set theory to explain probability," I wrote above, but "What is probability?" Set theory is useful for illustrating. The explanation that "an event treated as a probability is part of the whole" is set theory itself.
Therefore, there seem to be two ways in which probability and set are connected. One is the connection via measure theory that probability is a type of measure. Sets are used to describe measures.

The other is that probability is a quantity that originally represents the relationship between the whole and the parts of the set. Sets are used directly to explain probabilities.
I wrote two probability theories that come out of set theory, but I feel like there is another one. Set theory assumes that the set of the whole has some fixed property and that it is uniform throughout the whole.
In the real world, when people think of probabilities, the point seems to be that they assume that there is a whole set, but it is not uniform.
In mathematics class, probability and integral are studied as if they were different disciplines, but in measure-theoretic probability theory, they go together.
First of all, the probability is added to 1, so the integral comes out when the operation of "adding" is advanced.
In addition, statistics such as the mean value are calculated as a type of expected value, but since the calculation of the expected value is the sum of all probabilities, integration appears in this calculation as well.
The view of space can be expanded in the following order: length, area, and volume. In the case of probability, it has properties similar to area, but the difference is that vertical and horizontal units are not the same, like area in space.
"Measure theory is the foundation of probability theory. Probability theory is the foundation of statistics. Statistics is the foundation of data science. Therefore, it seems that the general explanation is that measure theory is the basis of data science.
As the author, "Measure theory deals with what it means to 'measure,' which is what data is. Therefore, I think there is an explanation that measure theory is the foundation of data science. When I think about this relationship, I don't talk about probability.
It's not that one is right, but I think there are two ways of thinking. For example, when there is data of "1.5 mm", the former view is "probabilistically obtained". From the latter point of view, it is "something that has been measured and obtained."
Probability theory has been studied in various ways by incorporating measure theory. However, such research seems to be being conducted with an interest in mathematics, and it does not seem to be useful for themes such as those that data science deals with.
On the Distinguishing and using data page, we have written "size data and position data" and "additive and non-additive" as distinctions for quantitative data. This distinction also becomes, "Does it apply to the measure of measure theory?"
I've written a little more about it on the Distinguishing and using data page, but this distinction expands the application of data science.
Measure theory is a discipline that deals with "measuring", but it does not deal with the act of "measuring". For quantities like length and area, It deals with mathematical definitions of "what is measured" and "what is measured".
The act of "measuring" comes to measurement engineering, but for example, in the case of length, the standard of "this is 1 mm" is determined. "Measuring" means looking at the size of the object you want to measure against that standard. When measuring, we sometimes use the laws of physics and regression analysis, and in such cases, mathematics is used, but we do not use measure theory.
Measure theory does not aim to obtain the magnitude of a specific quantity, so the idea of "what about the standard?" does not appear.
The measure theory does not appear in measurement engineering books that I read. Measure theory is a discipline that has studied "length". Even when it comes time to measure length, there is no measure theory.
However, it seems that it is not possible to say that "measure theory is unnecessary when actually measuring something".
In the world of elementary particles and the world of space, which deals with things that are not familiar to us, it seems that measure theory has a lot to do with researching what can be measured and what we want to measure.
Lebesgue integrals are a type of so-called integrals.
The integral taught in high school is called the Riemann integral, and the Lebesgue integral is an even more powerful version of it. An example that cannot be integrated with Riemann integrals but can be handled by Lebesgue integrals is the Dirichlet function.
Measure and integral are inseparable. If the measure is not defined, the integral cannot be defined, and the measure itself is made up of the idea of integrality, which is "adding up".
Measures seem to have been born out of rethinking integrals.
In the world of probability theory, integrals often come up. This is because the calculation of the expected value, such as the average value, is integral.
To change the subject, measures and Lebesgue integrals have been studied together. If we think of probability as a type of measure, then "Lebesgue integral is suitable for dealing with probability".
Then, when approaching phenomena that are actually happening using the idea of probability, is it necessary to know Lebesgue integrals instead of Riemann integrals? That doesn't seem to be the case. In the Lebesgue integral manual, the integral of advanced functions appears, but the integral that appears in probability theory is not so advanced.
Similar to the above "Use of measure theory in acquiring data", there may be situations where Lebesgue integrals are very useful in integrals in the world that deal with things that are not familiar to us. I don't feel like I'm in society or in a company.
