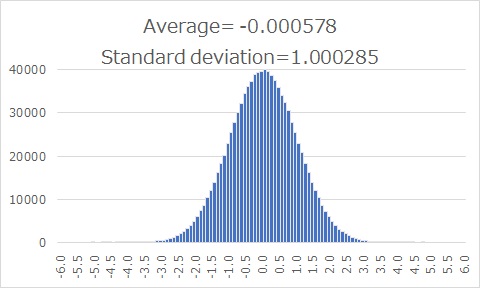
The histogram above is a histogram of 100 million samples (n=1000000). Since it is made to be normally distributed by random numbers, it has a clean normal distribution.
One of the important things when dealing with real data, although it does not appear in the world of statistics, is Significant Figures information.
Using significant figures helps you avoid getting into unrealistic stories.
The histogram above is a histogram of 100 million samples (n=1000000). Since it is made to be normally distributed by random numbers, it has a clean normal distribution.
It has a mean of -0.000578 and a standard deviation of 1.000285. The confidence interval is (-0.002018, 0.001903).
By the way The data used here is like the one below, and there are many digits.
In the case of desk calculations, this is the story, but there is no real data like this. Data such as physics experiments and factory measurements First of all, even one significant digit cannot be obtained. When you take care to manage the measurement system, it is usually about two digits. Maintaining three-digit accuracy can be quite challenging. By the way, Ferimi Estimation is a world where significant figures are expanded with about one digit.
If the significant figure is two digits, it will be up to the first decimal place, so For data like this example, the mean is 0.0, the standard deviation is 1.0, and the confidence interval is zero (none) or range of resolution.
When testing the difference in the mean value, the argument is "Can we say that there is a difference?"
Sometimes we ask ourselves, "Is it possible to say that there is a difference between the average value of 1.001 and 1.003?" If you check the significant figures and both are 1.0, you will be able to say "there is no difference" even if you do not test.
If you proceed without considering significant figures, you will suffer in a world of slight differences in mean values and the width of confidence intervals.
There is a page called Impossibility of data science, but significant figures make it impossible to take a statistical approach. I think it can be said that it is "the impossibility of statistics."
The range that humans can measure and perceive is the cause of impossibility.
However, I think this impossibility is a grateful property because it simplifies verification by testing.
NEXT 
Estimation of the capacity required for the measurement system (Estimation of significant figures)
