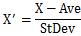
The method of statistical data analysis does not care about the unit of variables, only the size of numbers. For this reason, it may be noticeable in the analysis that the number is a large variable, even though it is a variable that does not make much sense.
Both standardization and normalization are convenient ways to treat variables equally in the analysis of mixed data of variables of different units.
Standardization subtracts the average (Ave) from the original data and divides it by the standard deviation (StDev).
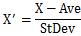
The data group that has undergone this conversion has a mean of 0 and a standard deviation of 1, and is dimensionless.
In standardization, the mean is subtracted and then divided by the standard deviation, but if you just subtract the mean, it is sometimes called "centralization".
Centralization can be used as a way to align the centers and make the difference in distribution easier to understand when the unit is the same for each variable but the distribution is different.
Normalization subtracts the minimum value (Min) from the original data and divides it by the range. The range is the difference between the maximum value (Max) and the minimum value.
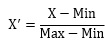
When normalized, the number is between 0 and 1. Multiplying by 100 will be between 0 and 100, which may improve the visibility of the numbers because you don't have to worry about the details after the decimal point.
Normalization can be useful because the numbers are between 0 and 1 and have a fixed range. You can use it when you want to treat all variables in the same way, or when you want to know where each sample is in the range.
With standardization, the range is different for each variable. With standardization, most samples fall in the range 0 to 1, and the more outliers are, the much larger the number, so you can use it when you want to include the outliers perspective in your analysis.
NEXT 
Standardization and Normalization with PCA
