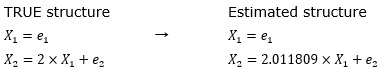
LiNGAM is a breakthrough method, but it also has its limitations. I tried to summarize what I noticed using.
In addition, since "NG" named " LiNGAM " is "Non-Gaussian (non-normal distribution)", it makes me want to think that "the limit is that the normal distribution cannot be used". But it is not valid, see the page, Distribution for which LiNGAM is effective.
The example on this page is about doing LiNGAM with a library called pcalg in R. I don't know if any LiNGAM is characterized by the same results.
The limits on this page are confirmed by the uniform distribution of the non-normal distribution, so it is the limit of LiNGAM regardless of whether it is a normal distribution or not.
First, an example when LiNGAM is not at its limit.
When the error terms e1 and e2 are uniform random numbers, LiNGAM gives the following result.
The left side is the formula for creating the verification data, and the right side is the result of LiNGAM. Assuming that the coefficient "2" is "2.011809", the numbers that roughly match are obtained.
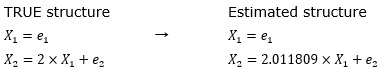
When doing this calculation, e1 and e2 use the R formula
runif(10000)
to find 10000 uniformly distributed random numbers.
When trying the LiNGAM method, the variability of the error terms should be about the same, but otherwise the output that LiNGAM expects cannot be achieved.
This is an example when the variation of e2 is 100 times that of e1.

The coefficient "2" cannot be obtained. The inferred formula means "X1 and X2 are independent".
Due to the large error term of e2, it is estimated to be "0 (no effect of X1)".
In the above example, if the coefficient of X1 is large to some extent, it will not be buried in the size of the error term, so the desired coefficient can be obtained.
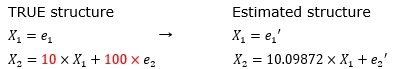
This is an example when the variation of e2 is 0.01 (1/100) times that of e1.
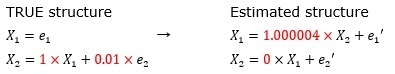
If the error term of e2 is too small, it cannot be distinguished from the state without the error term, and the place where the coefficient is not 0 cannot be specified.
In the above example, if the coefficient of X1 is large to some extent, the desired coefficient can be obtained.

If the coefficient is smaller than "2", it will not be obtained.
This is an example where the coefficient is "0.02".

Due to the large error term of e2, it is estimated to be "0 (no effect of X1)".
In the above example, if the error term becomes relatively small, it will not be buried in the size of the error term, so the desired coefficient can be obtained.
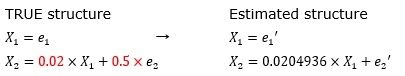
In the above "when the coefficient is extremely small, it is okay", "when the error term is relatively small, it is okay", but when the error term becomes smaller than the above example, a new limit is reached. Will be.
The coefficient of the error term is changed from "0.5" above to "0.2".
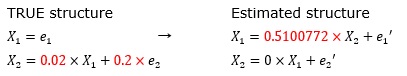
In the case of this example, not only the coefficient becomes 0, but also the place where I want another coefficient to become 0 is no longer 0.
NEXT 

 Relationship analysis of variables with LiNGAM
Relationship analysis of variables with LiNGAM
