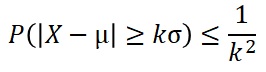
Chebyshev's inequality is the following equation: It shows that when there is a random variable X, u(myu), and standard deviation s(sigma), the probability is obtained by the number k.
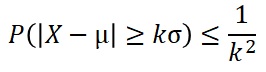
For example, when the mean is 0 and the standard deviation is 1, the probability of being outside the range of -2 to 2 is: Since k on the left side represents the time of 2, if you put it in the right side and calculate it, you can see that it is "less than 0.25".
The interesting thing about Chebyshev's inequality is that "any distribution holds." It is an estimate with low accuracy, but it can be calculated that it is "at least less than this value".
Chebyshev's inequality is characterized by "any distribution holds" and "low accuracy". Therefore, I tried to verify what it means to say that "any distribution holds" and how low the accuracy is.

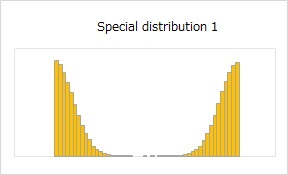
I examined three types of distributions. Once we know the normal and uniform distributions, I can guess what the generally known distribution will look like, so we chose these two first. Special distribution 1 is a distribution created by dividing the normal distribution into two in the middle and shifting it. Normal and uniform distributions are calculated because they are analytically accurate. For Special Distribution 1, 100,000 random number data were created and counted.
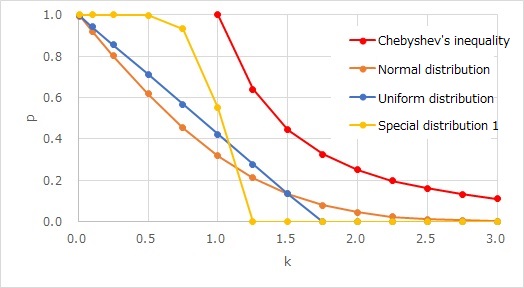
First, it turns out that if k is less than 1, then the probability is calculated greater than 1, so Chebyshev's inequality is completely useless.
When k is 2, the probability of a uniform distribution or special distribution 1 is 0. If it is the inequality of Chebyshev's inequality, it will be 0.25, which is about 5 times more than the normal distribution.
In the case of the standard normal distribution, what the probability will be when k = 1, 2, 3 is often used in practice. It is also called 1s, 2s, 3s, etc. If the distribution is somehow close to the normal distribution, it is a good guide. 1s is 0.3 (30%), 2s is 0.05 (5%), and 3s is 0.003 (0.3%).
It is not directly related to Chebyshev's inequality, but according to the above verification, if the distribution is uniform or special distribution 1, where there are precipices at both ends, You can see that around k=2, it is 0. This is a guide when the distribution is completely different from the normal distribution.
