トップページ |
統計学の解釈学 |
このサイトについて
トップページ |
統計学の解釈学 |
このサイトについて
以下は、筆者の私見です。 誤解があれば、ご教示いただけると幸いです。
シングルケースデザイン や 変化点検知 の文献で見かけたことがあるのですが、 自己相関 には誤解があります。
時系列分析では、株価のような金融関係のデータが、よく出て来ます。 このようなデータは、ある瞬間のデータに、足したり引いたりして次のデータが決まるので、 隣接サンプルのデータは因果関係があります。 また、自己相関も高くなります。
話は変わりますが、例えば、下の折れ線グラフは、
シングルケースデザイン
のページに同じものがあります。
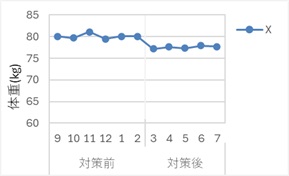
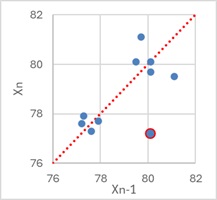
上の折れ線グラフのデータについて、それぞれのサンプルの値をY軸、そのひとつ前のサンプルの値をX軸として散布図を作ると、下のようになります。
赤丸があるサンプルは、変化点のところのサンプルです。
このサンプルが例外ですが、それ以外は、だいたい直線的に並んでいます。
つまり、これは自己相関があるデータです。
このデータでは、自己相関が高いからと言って、隣接サンプルと何か特別な関係があるとは限らないです。 例えば、この例が体重ではなく、同じ物を定期的に測った重さで、変化点は測定器の校正の場合が考えられます。 対策前、対策後のそれぞれの期間の中での値は、測定誤差なので、隣接サンプルとは何の関係もないです。
「相関関係と因果関係は異なる」は、 統計的因果推論 の解説で、「必ず」と言って良いほど紹介されます。
その話は、自己相関についても同じなのですが、忘れられていることが多いようです。
「自己相関があるのなら、隣接サンプルとは、何か特別な関係がある」という誤解が起こる原因としては、時系列データなことが考えられます。
因果関係の検証では、「原因の方が、先行する」ということがポイントのひとつです。 ここには、時間的な考え方が入っています。 このことと、「隣接サンプルと値が近い」という自己相関の性質が、混同されているのかもしれません。
