因果の時間差

定量的な仮説の探索は、相関関係の探索が基本です。この探索がうまく行く場合と、行かない場合をまとめてみました。

このページの例は、AとBの２つの変数のデータが、１時間毎に１日分あります。 Aが「原因では？」と疑っている変数で、Bが結果の変数とします。

うまく行く場合

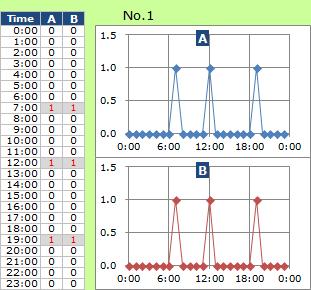
因果の時間差
No.1のようなデータの場合、つまり、同じ行に似たような事が起きている場合、相関が非常に高くなり、うまく行きます。

「Aは、Bとタイミングが同じ。よって、AがBの原因か、または、AとBに共通の原因があるのでは？」、と考察を進める事ができます。

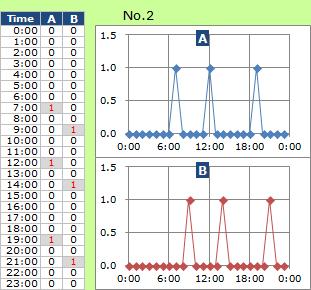
因果の時間差
No.2のようなデータの場合、グラフからは、AとBは同じようなタイミングで起きているように見えますが、相関は非常に低いです。

しかし、データをよく見ると、Bが1になるタイミングは、必ずAの2時間後です。 2時間分データをずらして、相関係数を計算すると、相関が非常に高い事が確認できます。

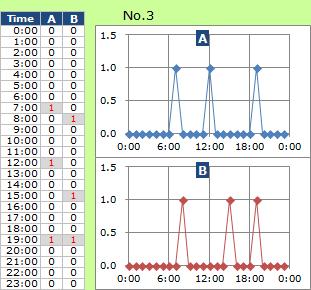
因果の時間差
No.3のようなデータの場合、グラフは、No.1やNo.2と似ています。しかし、相関は非常に低いです。また、No.2のようにデータをずらせば、うまく行く訳でもないです。

「原因系は、結果系よりも前に起きているはず」という事に気が付けても、相関係数のようなもので、このような相関の高さを表現する事は、とても難しいです。

No.3の例は、相関関係の探索の難しさが、わかりやすいです。

わかりやすくなるのは、0と1しか値がないためです。連続的に変化しているような値の場合は、タイミングのずれが多少あっても、相関が極端に低くなるような事は起きにくいです。

このページは、明らかに因果関係がありそうなのに、相関が低くなる場合を取り上げて来ましたが、相関が高いからと言って、必ずしも、タイミングをうまく把握できていない事もあります。

相関係数などを駆使して、因果関係を分析すると、上記のような難しさがあります。このような事に悩んでいては、「Bの変化」という結果はいつまでも解決しません。

今回のデータについて、例えば、筆者でしたら、
「Aの特徴は、7:00、12:00、19:00、これって食事の時間帯では？」
というように、まず考えます。

すると、
「食事の時間帯に起きる何かがBの原因では？」
というように、考えが進みます。

手っ取り早く、問題解決を進めるのなら、具体的なデータの意味に踏み込むのが、ひとつの方法です。

時間差をきちんと考えて、紐付けできるのなら、それに越した事はありません。

ただ、時間差の中での変化より、データ全体の中での変化の方が、ずっと大きい場合は、 Bの時刻と同じ時刻のAのデータを紐付けたとしても、正確に紐付けた時とほとんど変わらない分析ができる事があります。

相関関係による仮説の探索は、No.1のようなデータならうまく行きます。 No.1がうまく行くのは、同じ行に原因と結果のタイミングが入っているからなので、データをそのように作りこんでしまうと良いです。そうすれば、相関係数などは、使い勝手の良い指標になります。

この方法のひとつが、逆時間集計です。