トップページ | ひとつ上のページ | 目次ページ | このサイトについて | ENGLISH

真の平均値の差と、分析方法の関係

平均値の差の検定 では、データを使って、「平均値に差があると言えるのか？」を調べます。 データを見ているだけでは絶対にわからないのですが、データからわかる平均値は、「真の値に近いだろう」と考えている値です。

普通は、真の値は何かがわからないものの、そういう値があることを前提にして、分析します。 そのため、「平均値の差について、「真」の値があった場合、そこからサンプリングすることで調べて、どれだけ真に迫られているのか？」ということは、 普通はわかりません。

そこで、シミュレーションで調べてみました。

平均値が０のグループと１のグループで、両方とも標準偏差が１になっている乱数を発生させて調べます。 そのため、平均値の差が１というのが、真の値になります。

効果量の分布　（コーエンのd）

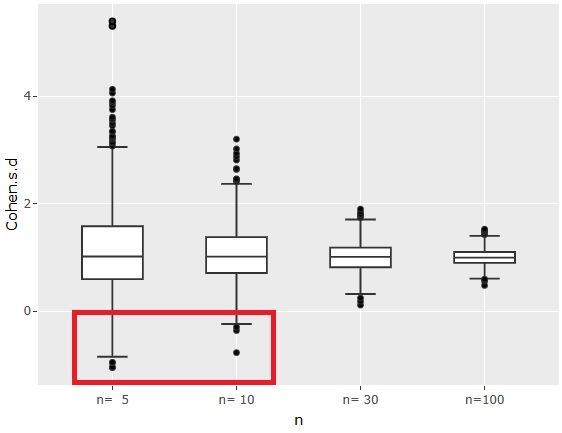
まず、効果量は、上のグラフのようになりました。 効果量は、絶対値を使わないで計算しています。

サンプル数に関わらず、効果量は１が中心になるのは、平均値の差が１で、標準偏差が１になっているところから決まっています。

サンプル数nが5や、10の時は、効果量がマイナスになる場合、つまり、平均値の大小が逆転するようにサンプリングされる場合があることがわかります。

平均値の差の検定（t検定）

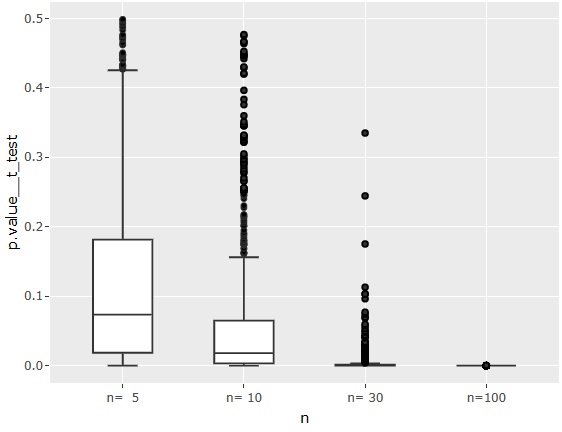
一般的な平均値の差の検定 のp値です。

n=5の場合は、中央値が0.05よりも高いので、真の平均値の差が１くらいだと、「差がある」という判定になりにくいことがわかります。

n=100の場合は、確実に「差がある」と判定されます。

正規分布の差の検定１

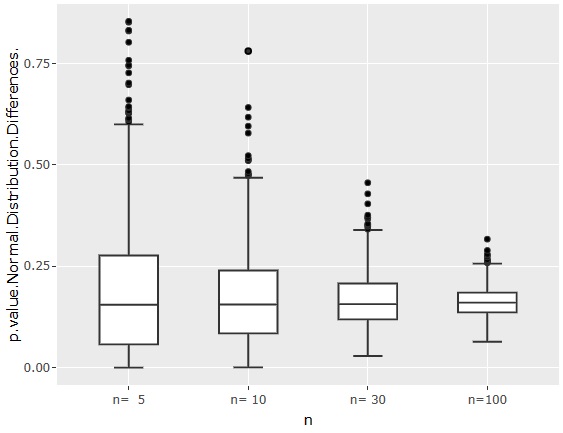
正規分布の差の検定 のページで１番目に書かれている手法の場合のp値です。

n=100でも、p値が0.25くらいの時があるので、「p値は0.05を目安」という感覚から考えると、「差がある」という判定をするには、かなり厳しく見ている方法であることがわかります。

効果量と正規分布の差の検定１の関係

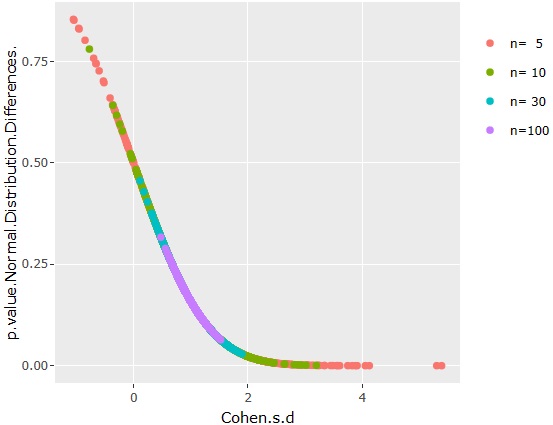
効果量と正規分布の差の検定１の関係を散布図にすると、上のグラフになります。

効果量や、正規分布の差の検定１は、サンプル数nに関わらずに重なっているので、これらの尺度はサンプル数の影響を受けていないことがわかります。

実際のデータと、統計学的な方法の関係

このページの上記の方法から考えると、n=5や10くらいで意思決定をするのは、デタラメとも言えるような気がします。 最低でも100くらいないと、判断できない感じです。

一方で、筆者が工場関係のデータで今までに経験した中では、n=5くらいで判断して、その後にデータが増えてから、「あの判断は、間違いだった」となったことはないです。

ということは、「データとは、真の値や分布と言えるものがあって、そこからランダムにサンプリングしたもの」という統計学の前提と実際が合っていないようです。

順路 次は スモールデータの検定の効果量