以下は、筆者の私見です。 誤解があれば、ご教示いただけると幸いです。
ネットの記事ではなく、教科書のようにして、出版されている本でも、 「サンプル数が多い時は、正規分布。少ない時は、t分布」という説明を見かけます。
これは、統計学の正式な説明としては間違いですが、実務向きの認識としては間違いではないです。 その理由は、ややこしいです。以下にまとめてみました。
t分布は、正確には、分散が未知かどうかは、もともと関係なく、母平均が既知の時に、データが従っている分布です。 分散が既知の時には、正規分布があるので、 「分散が未知の時にも成り立つ」という特徴に対して、「分散が未知の時に使う」という説明になっています。
正規分布とt分布の使い分けは、分散が既知か、未知かの違いに対してします。 このように説明している教科書が、とても多いです。
これは、正規分布は、母分散を含む分布、t分布は母分散を含まない分布であるためです。
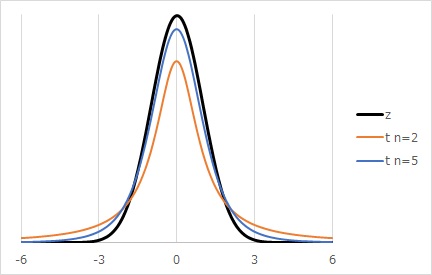
t分布には、「サンプル数が多いと、正規分布に近付く」という特徴があります。
これの理解として、「サンプル数が多い時は、t分布と正規分布の区別がいらない。少ない時は、t分布の方が厳密」という解釈をしているように見受けられる説明を見かけます。
「サンプル数が多いと、正規分布に近付く」という性質の理解だけで、使い分けをしているのなら、誤解です。
しかし、実務向きの認識としては、サンプル数で判断しても間違いではないです。
既知と未知の使い分け のページに、詳しく書きましたが、実務では、既知か未知かに関わらず、近似理論として正規分布を使うためです。
「近似理論」と思っているのなら、「サンプル数が多い時は、正規分布。少ない時は、t分布」という理解は、実務向きの認識としては、間違いではないと思います。
ちなみに、この考えに基づけば、t分布を一切使わない流儀もあるかと思います。
ただ、サンプル数が一桁くらいの時は、正規分布とt分布の違いは、それなりに大きいので、サンプル数が少ない時だけは、t分布を使うのは汎用性が高いです。
