setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
pairs.panels(Data) # グラフにする
部分的最小二乗回帰分析 の使い方の紹介になります。
CドライブのRtestというフォルダに、Data.csvというファイルがある状況を想定しています。 目的変数は「Y」という名前になっている必要があります。 Y以外のすべての変数を主成分分析するようになっていますので、説明変数の名前はなんでも良いです。
library(psych) # ライブラリを読み込み
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
pairs.panels(Data) # グラフにする
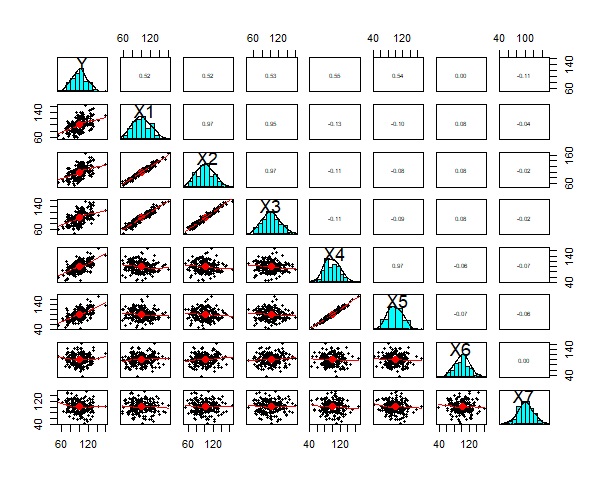
X1、X2、X3間も相関があることがわかります。
X4とX4は、相関があることがわかります。 YとXの相関は、何となくありそうにも見えますが、よくわからない感じです。
X6とX7は、どれとも相関がないらしいことがわかります。
md<-step(lm(Y~.,data=Data))# 重回帰分析（step関数で変数の選択）
summary(md) # 結果
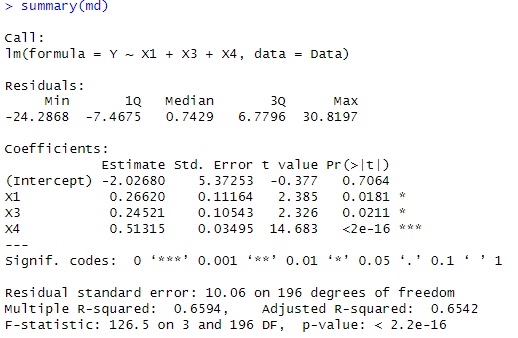
普通の重回帰分析で調べたところ、X1、X3、X4で作ったモデルがベストということがわかりました。 X1とX3は相関が高いので、どちらか片方になってもおかしくないですが、ステップ関数で変数の選択をすると、X1とX3の両方が残りました。
この分析方法だと、「X2、X3はX1と相関があるから・・・」、というような考察になります。
主成分回帰分析 です。
library(pls) # ライブラリを読み込み
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
pls_model <- plsr(Y~.,data= Data)# PLS
summary(pls_model) # 結果
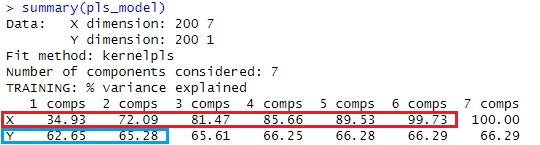
説明変数のXについては、累積寄与率が99%になるまでには、主成分が６個必要なことがわかります。
また、目的変数と説明変数の相関は、第２主成分以降が加わっても、累積寄与率があまり増えていないです。 そのため、第１主成分のみで求まるモデルで、ほとんど決まっていることがわかります。
この例の場合は、累積寄与率（Cumulative Proportion）がPC4までで98%になっているので、４個の成分で回帰分析をすることにします。
Data1 <- Data
Data1$Y <- NULL
nc <- ncol(Data1)
nr <- nrow(Data1)
scr <- pls_model$scores
scr <- scr[1:nr,]
Data1scr <- cbind(Data1,scr)
cor2 <- cor(Data1scr)^2# 寄与率を計算
cor2 <- round(cor2[nc+1:ncol(scr),1:nc],4)# いらない部分を取る
cor2 # 結果を出力
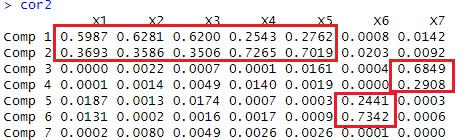
この結果を見ると、
Comp1と2で、X1,2,3,4,5が表されていて、Comp1と2の割合の違いが、X1,2,3のグループと、X4,5のグループの違いになっています。
pc3 <- cor2 # 寄与率（相関係数の２乗）を計算
pc3[pc3 < 0.1] <- 0 # 寄与率が以下の関係は見ないことにする
pc3
library(igraph) # パッケージを読み込み
pc4<-pc3*10 # 線の太さを変更
DM.g<-graph_from_incidence_matrix(pc4,weighted=T) # グラフ用のデータを作る
V(DM.g)$color <- c("steel blue", "orange")[V(DM.g)$type+1] # 色を変える
V(DM.g)$shape <- c("square", "circle")[V(DM.g)$type+1] # マークの形を変える
plot(DM.g, edge.width=E(DM.g)$weight) # グラフを作る
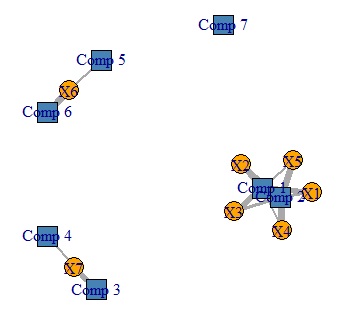
表のデータが、グラフで見やすくなりました。
