Rによるデータ分析
Rによるデータ分析
 Rによるデータ分析
Rによるデータ分析
有向条件付き相互情報量分析 のRによる実施例です。
基本的に質的変数を扱う方法ですが、量的変数は 1次元クラスタリング の方法で、質的変数に変換するコードが入っているので、 質的・量的が混合していたり、量的変数だけでも使えるようにしてあります。
library(igraph)
setwd("C:/Rtest")
Data <- read.csv("Data.csv", header=T) # データを読み込み
Data1 <- Data
n <- ncol(Data1)
for (i in 1:n) {
if (class(Data1[,i]) == "numeric" | class(Data1[,i]) == "integer") {
Data1[,i] <- droplevels(cut(Data1[,i], breaks = 3,include.lowest = TRUE))# 3分割する場合。量的データは、質的データに変換する。
}
}
# 相互情報量行列を計算する関数
mi_matrix <- function(data) {
vars <- colnames(data)
p <- length(vars)
result <- matrix(0, nrow = p, ncol = p)
colnames(result) <- vars
rownames(result) <- vars
for (i in 1:p) {
for (j in 1:p) {
if( i >= j){
TableXY <- table(data[,i], data[,j])# 分割表の作成
Px <- TableXY
for (k in 1:nrow(TableXY)) {
Px[k,] <- sum(TableXY[k,])/sum(TableXY)
}
Py <- TableXY
for (k in 1:ncol(TableXY)) {
Py[,k] <- sum(TableXY[,k])/sum(TableXY)
}
Pxy <- TableXY/sum(TableXY)
pMI <- Pxy*log(Pxy/Px/Py,2)
pMI[is.na(pMI)] <- 0
MI <- sum(pMI)
k <- min(ncol(TableXY), nrow(TableXY))
MI <- sum(pMI)
result[i,j] <- MI
result[j,i] <- MI
}
}
}
return(result)
}
# 条件付き相互情報量を計算する関数
cmi <- function(X, Y, Zdf, logbase = exp(1)) {
Z_comb <- interaction(Zdf, drop = TRUE)
df <- data.frame(X = X, Y = Y, Z = Z_comb)
p_xyz <- prop.table(table(df$X, df$Y, df$Z))
p_xz <- prop.table(table(df$X, df$Z))
p_yz <- prop.table(table(df$Y, df$Z))
p_z <- prop.table(table(df$Z))
result <- 0
for (i in seq_len(dim(p_xyz)[1])) {
for (j in seq_len(dim(p_xyz)[2])) {
for (k in seq_len(dim(p_xyz)[3])) {
pxyz <- p_xyz[i,j,k]
if (pxyz > 0) {
pxz <- p_xz[i,k]
pyz <- p_yz[j,k]
pz <- p_z[k]
result <- result +
pxyz * log((pxyz * pz) / (pxz * pyz), base = logbase)
}
}
}
}
return(result)
}
# データフレームからCMI行列を作る関数
cmi_matrix_all <- function(data, logbase = exp(1)) {
data[] <- lapply(data, as.factor)
vars <- colnames(data)
nvar <- length(vars)
mat <- matrix(NA, nvar, nvar)
rownames(mat) <- vars
colnames(mat) <- vars
for(i in seq_len(nvar)) {
for(j in seq_len(nvar)) {
if(i != j) {
cond_vars <- setdiff(vars, c(vars[i], vars[j]))
mat[i,j] <- cmi(
data[[vars[i]]],
data[[vars[j]]],
data[, cond_vars, drop = FALSE],
logbase = logbase
)
}
}
}
return(mat)
}
cor2 <- mi_matrix(Data1)
pcor2 <- cmi_matrix_all(Data1)
directed_cor2 <- cor2
n <- ncol(cor2)
# 2つの行列から、成分の小さい方を選んだ行列を作る。ただし、対角成分は相互情報量行列を使う
for (j in 1:n) {
for (i in 1:n) {
if(i < j){
if(cor2[i,j] < pcor2[i,j]){
directed_cor2[i,j] <- cor2[i,j]
directed_cor2[j,i] <- cor2[i,j]
} else {
directed_cor2[i,j] <- pcor2[i,j]
directed_cor2[j,i] <- pcor2[i,j]
}
}
}
}
round(cor2,3) # 相互情報量を出力
round(pcor2,3) # 条件付き相互情報量を出力
round(directed_cor2,3) #選択済みの情報量を出力
directed_cor3 <- directed_cor2 / log(n,2) # 標準化(カテゴリ数標準化型)
round(directed_cor3,3) # 標準化した情報量を出力
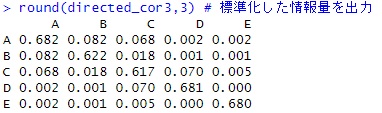
GM2 <- directed_cor3
directed_cor201 <- GM2
directed_cor201[,1:n] <- 0
for (i in 1:n) {
for (j in 1:n) {
if(i > j){
if(GM2[i,j] > 0.02){
diffGM2 <- GM2[i,i] - GM2[j,j]
if(abs(diffGM2) > 0.0001){
if(diffGM2 > 0){
directed_cor201[i,j] <- GM2[i,j]
} else {
directed_cor201[j,i] <- GM2[i,j]
}
} else {
directed_cor201[i,j] <- GM2[i,j]
directed_cor201[j,i] <- GM2[i,j]
}
}
}
}
}
directed_cor201
GM5 <- ceiling(directed_cor201)
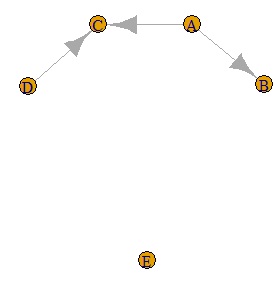
GM6 <- graph.adjacency(GM5,weighted=F, mode = "directed")
plot(GM6)