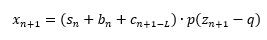外生変数付き三重指数平滑法（ETSXモデル） は、実務向きの時系列予測としては、三重指数平滑法（ETSモデル）に匹敵する方法です。
理由は、２つあります。
ここでは、ExcelのFORECAST.ETS関数を応用する方法を説明します。 この関数を使わずに、Excelで実行する方法もありますが、使った方がはるかに簡単です。
ホットケーキミックスを使うと、ホットケーキが簡単に作れることと似ています。
ETSXモデルでは、α、β、γのほかに、pやqといった係数を推定する必要がありますが、 α、β、γの推定は、FORECAST.ETS関数に任せ、それ以外を推定する仕組みを自分で用意します。
ETSXモデルのAAAA型と、AAAM型を説明します。
データを用意します。 4/1から4/10までは実測値があります。4/11から4/16が予測したい期間です。
zが外生変数で、イベントがある時が１になっています。 予測したい期間にも、イベントがある時は、１にしています。
なお、この例では、外生変数が０と１だけの変数ですが、例えば、温度のように様々な値になる変数でも、同様に扱います。
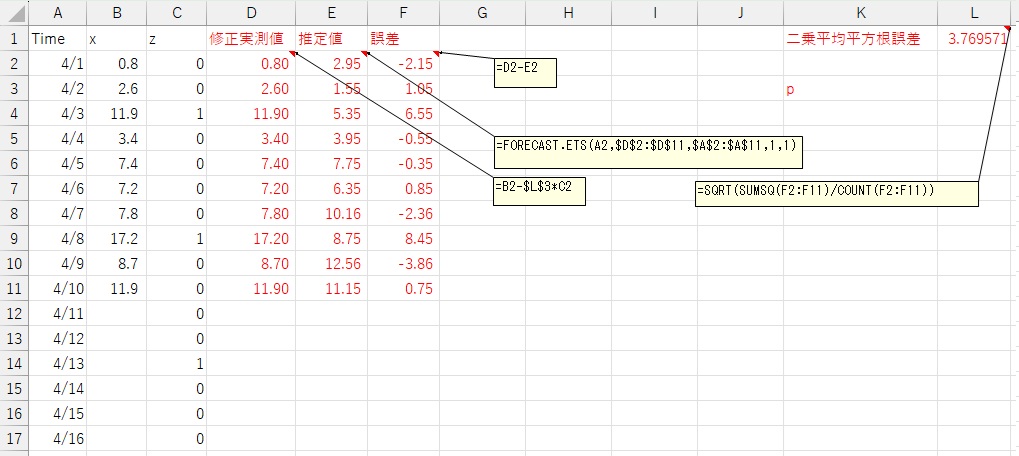
D、E、F列とL1列に関数を入力します。
FORCAST.ETSが参照する値を、D列にする点が、ETSXモデルのポイントです。
L3セルは、この最適化計算で埋まるので、この段階では、空白のままで良いです。
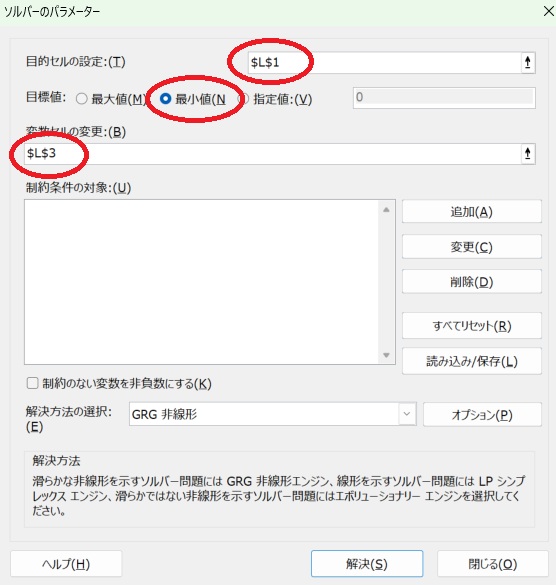
「データ」タブの「ソルバー」を選びます。
ソルバーのパラメーターを設定します。
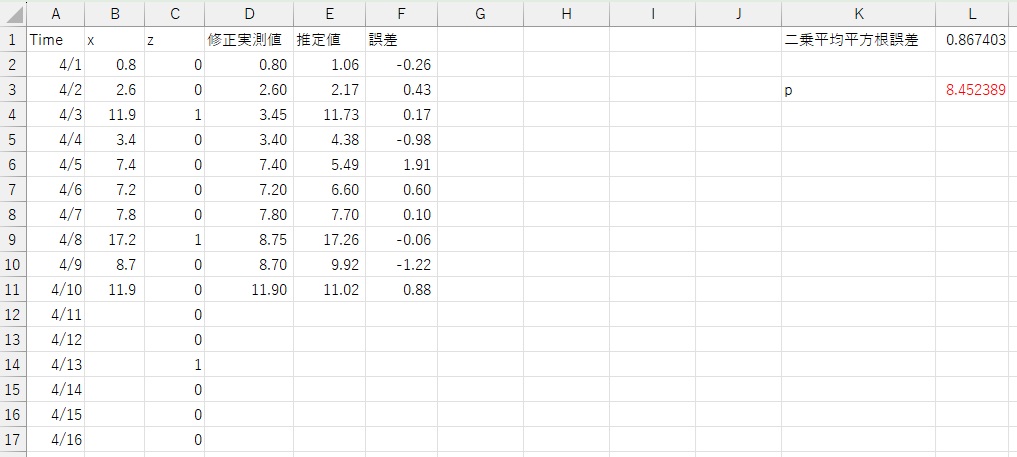
最適化された値がL3セルに出力され、それに伴って、計算値が更新されます。
G、H、I列に予測のための関数を入力します。
予測シートの出力と似ていますが、FORECAST.ETS関数に追加をしているところがポイントです。
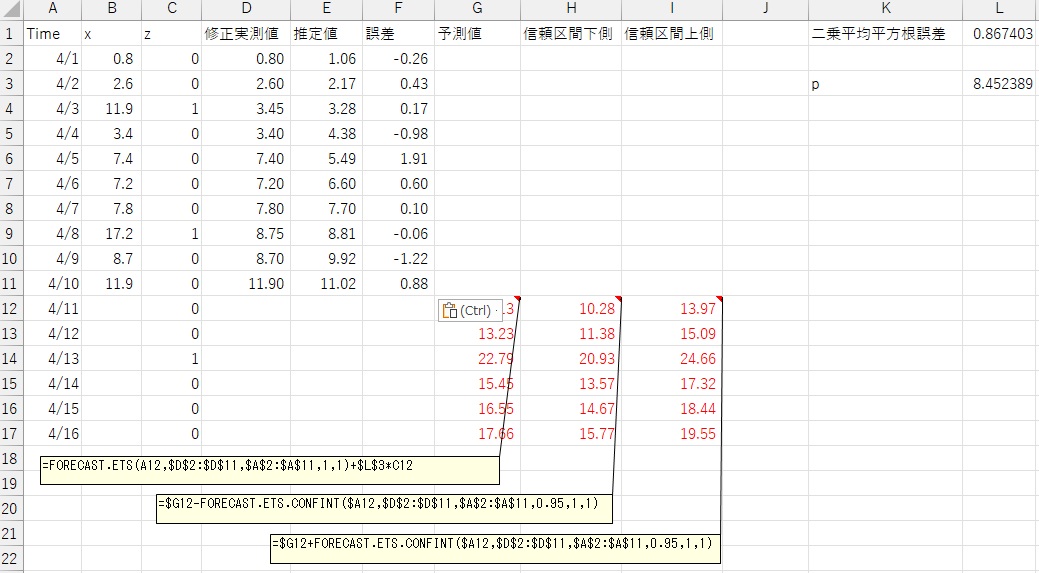
できたデータをグラフにします。
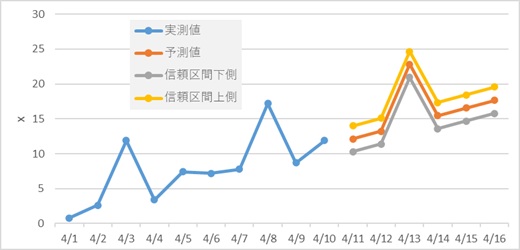
AAAM型では、以下のようにします。 AAAA型とほとんど同じですが、D、E、G、H、I列の式が異なります。
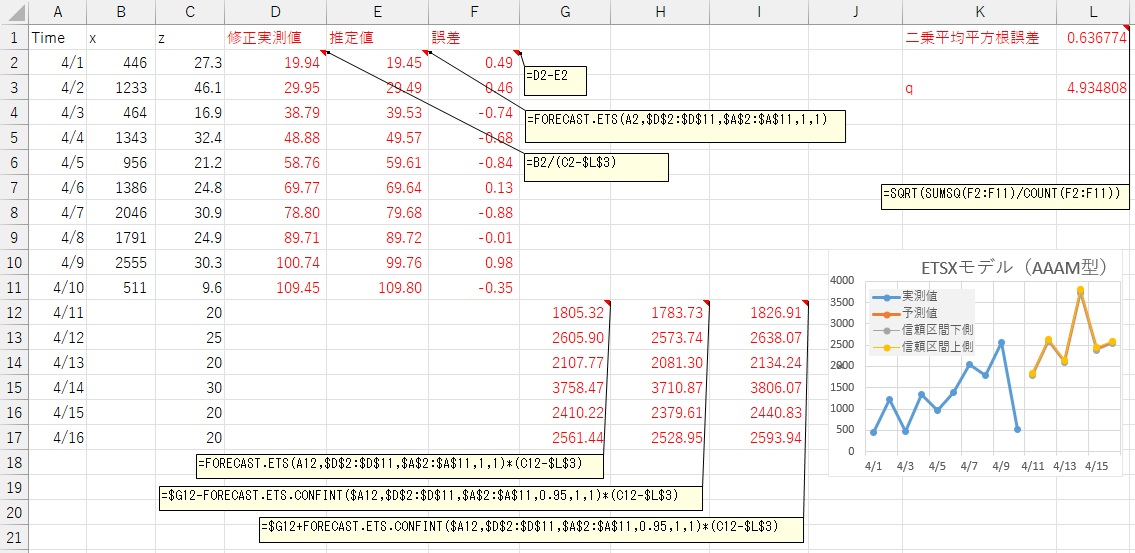
AAAM型の式は以下ですが、予測はpの値と関係なくできるため、計算では、pが出て来ません。
