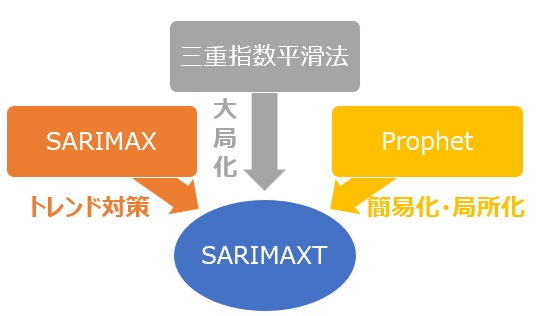
SARIMAXTモデルは、筆者が考えたモデルです。 先行研究があれば名前はそちらに合わせますが、なさそうなので、この名前にしています。
「SARIMAXTモデル」という名前からわかるように、 SARIMAXモデル の発展版です。
SARIMAXのXは、外生変数を表しますが、ここに時刻(Time)の関数を入れます。 そこで、SARIMAXTにしました。 SARIMAXの系統では、データの並び順を時系列として使うので、時刻や時間の変数があっても、計算で使いません。 SARIMAXTは、その変数を使います。
「SARIMAX」が名前に入っていますが、実体は
Prophet
と構造が似ています。
Prophetの簡易版のような方法です。
簡易版ですが、Prophetの弱点に対策した方法になっています。

Prophetは、季節項、トレンド項、イベント項の3つの足し合わせになっているところはわかりやすいです。
いずれもコンピュータ任せの手間のかかる計算をします。
Prophetは、季節項に三角関数を使います。
ところで、現実の季節性は、「日曜日だけ売上が下がる」、「月初だけ混雑する」というような感じなので、三角関数が表す正弦波のような変化になりません。現実に合わせようとすると、正弦波の重ね合わせが必要になり、モデルが複雑になります。
また、現実の季節性では、「最近数年の傾向」のようにして、近い過去と遠い過去で特徴が異なることがありますが、 三角関数は、近い過去も遠い過去も似ていることを前提にしています。 Prophetは、 季節性が大局モデル です。
SARIMAXTモデルでは、季節性は、1周期前のデータを変数にすることで扱います。 周期が2つあれば、加える変数は2つです。
たったこれだけで、季節性を扱えます。 また、近い過去を参照するモデルになるので、遠い過去の特徴が違っていても問題ありません。 つまり、局所モデルになっています。
Prophetは、トレンド項には区分線形回帰を使います。
現実のトレンドは、変化点を境にして直線の角度が変わるような変わり方よりも、カーブの方が自然です。
SARIMAXTモデルでは、例えば、全体を3次関数で近似するのなら、元の変数の3乗と2乗の変数をそれぞれ加えます。 たったこれだけで、トレンドを扱えます。
Prophetや 三重指数平滑法 と比べた場合、 SARIMAXモデルは予測値にトレンドを考慮できないところが弱点です。 SARIMAXTモデルは、この弱点に対策ができています。
三重指数平滑法 は、局所的な関数でできています。
SARIMAXTは、トレンドを大局的な関数で表します。
以下は、同じデータに対して、SARIMAXとSARIMAXTを適用した場合です。
SARIMAXTは、実測値の延長のようにして、予測できている様子がわかります。
SARIMAXは、トレンドが考慮できないため、だんだん上昇して行く様子が予測できません。
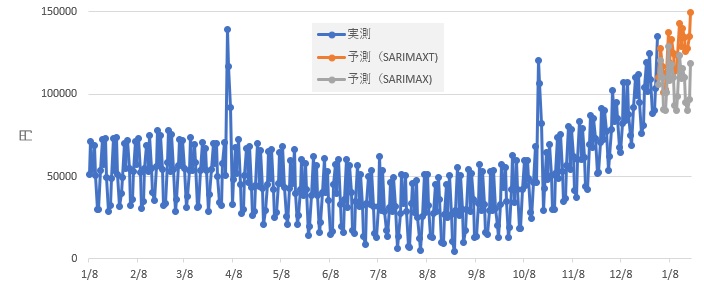
実測データの直後くらいなら、モデルの違いが出ませんが、時間が経過するほど、違いが大きくなります。
SARIMAXTモデルは、MAを含まないのなら、EXCELの重回帰分析の機能で扱えます。
ExcelでSARIMAXTモデル で、具体的な手順を説明しています。
「Forecasting: principles and practice, 3rd edition 予測: 原理と実践 (第3版)」 Hyndman, R.J., & Athanasopoulos, G. 著 OTexts 2021
https://otexts.com/fppjp/ets-forecasting.html
Prophetが簡単に説明されています。
順路


 次は
時間解析
次は
時間解析

