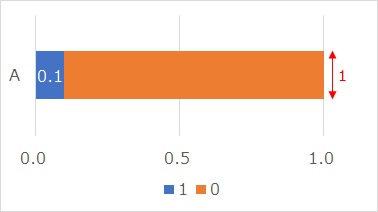
比率分布というのは、上のグラフのようなものです。
比率分布の重なりの検定は、 比率の全体的な差の検定 の一種です。
差による分布の重なりの検定 と似ているですが、分布の考え方がポイントです。
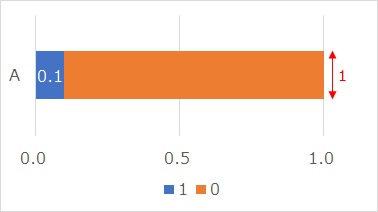
比率分布というのは、上のグラフのようなものです。
比率を計算するための元データは、例えば、「０が90個、１が10個」といった０と１だけのデータです。 この場合、１の比率は0.1となりますが、これが上のグラフの「0.1」の部分を表します。
このグラフは、グラフの帯の幅を「１」と考えると、面積が「１」となり、確率密度関数として使えます。 確率密度関数は、一般的に山型の分布で表しますが、比率の場合、元のデータが０と１しかないため、このようなグラフで確率密度関数が表せます。
なお、比率分布のこのような表し方は、筆者が考案したものです。 既に世の中にあるかもしれませんが、筆者は見たことがありません。 もしあれば、このページの内容は、それに合わせるつもりです。
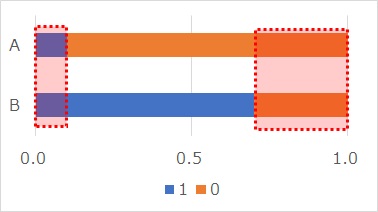
比率分布の違いの検定２では、p値の考え方が、基本的に正規分布の差の検定２と同じです。
２つの分布の共通部分の面積をp値とみなします。
２つの比率が、r2とr1で、r2の方が大きい場合、p値は以下の式になります。
p value = r2 + (1 - r1)
EXCELの場合、例えば、A2とB2というセルに２つの比率が入力されている場合、下の式でp値が求まります。
=1+MIN(A2:B2)-MAX(A2:B2)
順路
次は
相関係数の効果量の検定
