 Rによるデータ分析
Rによるデータ分析
 Rによるデータ分析
Rによるデータ分析
ベクトル量子化平均法 のRによる実施例です。
ベクトル量子化 で説明変数を1次元の質的変数に圧縮してから、 それを基にして集計します。 その後で、目的変数と結合します。
ここでは、以下のデータを使っています。
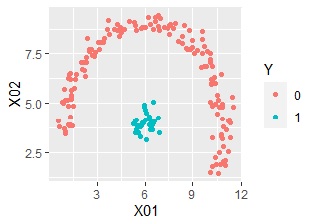
library(mclust)
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
Y <- Data$Y
Data10 <- Data
Data10$Y <- NULL# Yの列を削除
Data11 <- Data10 # 出力先の行列を作る
for (i in 1:ncol(Data10)) {
Data11[,i] <- (Data10[,i] - min(Data10[,i]))/(max(Data10[,i]) - min(Data10[,i]))# 正規化
}
mc <- Mclust(Data11,10) # 混合分布で分類。これは10個のグループ分けの場合
cluster <- mc$classification
cluster <- as.character(cluster)# 文字列に変換
cluster <- as.data.frame(cluster)# データフレームに変換
Data4 <-cbind(Y,cluster)# データセットの作成
Data6 <-aggregate(Y~cluster,data=Data4,FUN=mean) # クラスター毎に平均値を計算
colnames(Data6)[2]<-paste0("predicted_Y")
library(dplyr)
Data4 <-left_join(Data4,Data6,by="cluster")
colnames(Data4)[3]<-paste0("predicted_Y")
library(ggplot2)
Data4$Y <-NULL
Data2s2 <- cbind(Data,Data4)# データを読み込み
ggplot(Data2s2, aes(x=X01, y=X02)) + geom_point(aes(colour=predicted_Y)) + scale_color_viridis_c(option = "D")
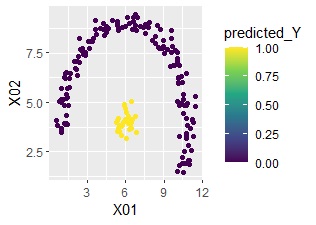
完璧に予測できていることがわかります。
下記で、クラスターがどのように作られたのかが、わかります。
ggplot(Data2s2, aes(x=X01, y=X02)) + geom_point(aes(colour=cluster))
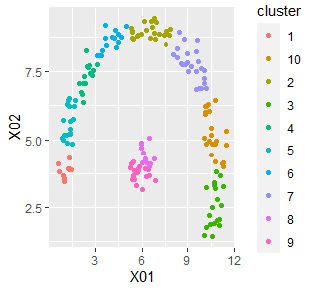
目的変数が量的変数の場合も、上記のコードで同じです。
学習用データは上記と同じです。テスト用データは下記の3つのサンプルになっていて、Data2.csvに入っています。
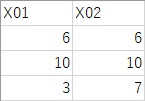
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
Y <- Data$Y
Data10 <- Data
Data10$Y <- NULL# Yの列を削除
Data11 <- Data10 # 出力先の行列を作る
for (i in 1:ncol(Data10)) {
Data11[,i] <- (Data10[,i] - min(Data10[,i]))/(max(Data10[,i]) - min(Data10[,i]))# 正規化
}
library(mclust)
mc <- Mclust(Data11,10) # 混合分布で分類。これは10個のグループ分けの場合
cluster <- mc$classification
cluster <- as.character(cluster)# 文字列に変換
cluster <- as.data.frame(cluster)# データフレームに変換
Data4 <-cbind(Y,cluster)# データセットの作成
Data6 <-aggregate(Y~cluster,data=Data4,FUN=mean) # クラスター毎に平均値を計算
colnames(Data6)[2]<-paste0("predicted_Y")
Data2 <- read.csv("Data2.csv", header=T)
Data21 <- Data2
for (i in 1:ncol(Data2)) {
Data21[,i] <- (Data2[,i] - min(Data10[,i]))/(max(Data10[,i]) - min(Data10[,i]))
}
output2 <- predict(mc, Data21)$classification
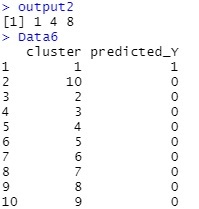
output2が、クラスターの予測値です。
Data2.csvというファイルのデータの順になっています。
Data6が、クラスター毎のYの予測値です。
例えば、2個目のサンプルは、クラスター4と予測されたので、Yの予測値は0だということがわかります。
CRAN
https://cran.r-project.org/web/packages/MASS/MASS.pdf
MASSのマニュアルです。
CRAN
https://cran.r-project.org/web/packages/nnet/nnet.pdf
nnetのマニュアルです。
「機械学習のための特徴量エンジニアリング」 Alice Zheng・Amanda Casari 著 オライリー・ジャパン 2019
名前はついていないのですが、ベクトル量子化回帰分析と同じ内容の方法が、ベクトル量子化の解説の後に、紹介されています。

