library(psych) # ライブラリを読み込み
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
#Data <- dummy_cols(Data,remove_first_dummy = FALSE,remove_selected_columns = TRUE)# ダミー変換
pairs.panels(Data) # 総当たりの散布図を作る
相関係数 を可視化する方法です。
変数の類似度の分析 です。
基本的に量的変数を扱う方法ですが、質的変数は ダミー変換 して質的・量的が混合していたり、質的変数だけでも使えるようにしてあります。
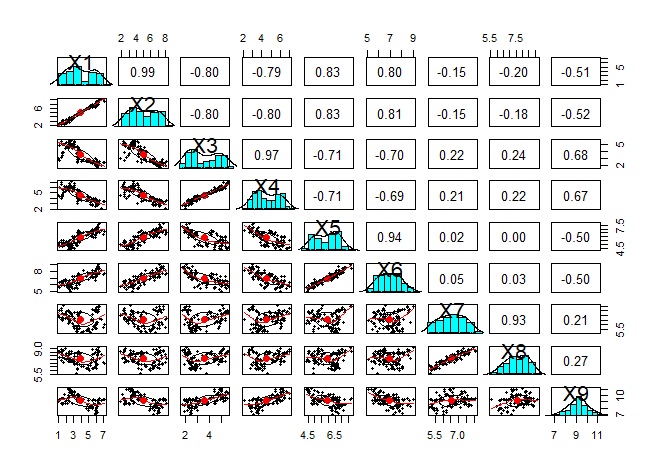
量的変数の類似度を見る方法として散布図は基本なので、 総当たりの散布図を見ることは大事です。
ただし、下記は変数が９個の場合ですが、たった９個でもこの後の分析が進めにくいグラフができあがります。 他の方法を使って、グラフにする変数は絞った方が良いです。
library(fastDummies)# ライブラリを読み込み
library(psych) # ライブラリを読み込み
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
#Data <- dummy_cols(Data,remove_first_dummy = FALSE,remove_selected_columns = TRUE)# ダミー変換
pairs.panels(Data) # 総当たりの散布図を作る
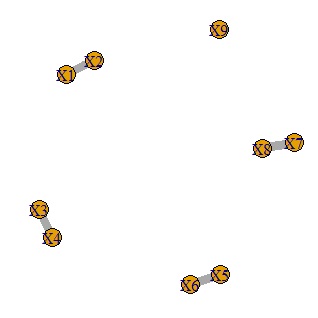
相関係数を計算して、相関の大きいものだけをネットワークグラフにする方法です。
library(fastDummies)# ライブラリを読み込み
library(igraph) #ライブラリを読み込み
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
#Data <- dummy_cols(Data,remove_first_dummy = FALSE,remove_selected_columns = TRUE)# ダミー変換
DataM <- as.matrix(Data) # テーブルデータを行列にする
GM1 <- cor(DataM) # 相関係数行列を計算
diag(GM1) <- 0 # 対角成分は0にする
GM2 <- abs(GM1) # 絶対値にする
GM2[GM2<0.9] <- 0 # 相関係数の絶対値が0.9未満の場合は0にする（非表示にするため）
GM3 <- GM2*10 # 一番大きな値が10になるように修正（パスの太さを指定するため）
GM4 <- graph.adjacency(GM3,weighted=T, mode = "undirected") # グラフ用のデータを作成
plot(GM4, edge.width=E(GM4)$weight) # グラフを作成
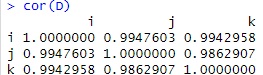
Rの場合、cor関数で、相関行列は簡単に作れます。
setwd("C:/Rtest")
D <- read.csv("Data.csv",row.names = 1) # １列目に行名が入っている場合は、こちらを使う
# D <- read.csv("Data.csv") # １列目に行名が入っていない場合は、#を取る
cor(D) # 相関行列
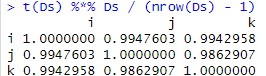
相関行列と内積 にある作り方です。
setwd("C:/Rtest")
D <- as.matrix(read.csv("Data.csv",row.names = 1)) # １列目に行名が入っている場合は、こちらを使う
# D <- as.matrix(read.csv("Data.csv")) # １列目に行名が入っていない場合は、#を取る
Ds <- D
n <- ncol(Ds)
for (i in 1:n) {
Ds[,i] <- (Ds[,i]-mean(Ds[,i]))/(sd(Ds[,i])) # 標準化
}
t(Ds) %*% Ds / (nrow(Ds) - 1) # 相関行列
