 Pythonによるデータ分析 |
Rによる隠れ変数の分析
Pythonによるデータ分析 |
Rによる隠れ変数の分析
 Pythonによるデータ分析 |
Rによる隠れ変数の分析
Pythonによるデータ分析 |
Rによる隠れ変数の分析
隠れ変数の探索 を、Pythonで進める時のレシピです。
因果推論 として 相関関係による仮説の探索 をやろうと思い、 Pythonによる変数の類似度の分析 をしたものの、注目している変数と他の変数の間には、何も相関が見つからないことがあります。
このページの方法は、そのような時に、あきらめずにさらにデータを探索するための方法になります。
主成分分析 と 独立成分分析 の2つの方法がありますが、同じような結果になることもありますし、 どちらかの方が、良いこともあります。
主成分分析を使う方法の方が、パラメタの設定がないですし、計算時間も短いです。 主成分分析では、隠れ変数が見つからない時に、独立成分分析を試すようにするのが良いようです。
下記のコードが注目している変数が「Y」ということにしています。 他の変数については、名前の付け方に決まりはありません。
import os #パッケージの読み込み
import pandas as pd #パッケージの読み込み
import matplotlib.pyplot as plt# パッケージの読み込み
import seaborn as sns # パッケージの読み込み
from sklearn import preprocessing # パッケージの読み込み
from sklearn.decomposition import PCA# パッケージの読み込み
%matplotlib inline
sns.set(font='HGMaruGothicMPRO') # PandasのPlotのグラフの見た目をseaborn風にする。グラフのフォントを設定する
os.chdir("C:\\PyTest") # 作業用ディレクトリを変更
df= pd.read_csv("Data.csv" , engine='python')# データを読み込み
df11 =pd.DataFrame(df['Y'])# Yの列を別に作っておく
df12 = df.drop('Y', axis=1)# Y以外の列を別に作っておく
df2 = pd.get_dummies(df12)# 質的変数はダミー変換
df3 = preprocessing.scale(df2)# 正規化
df3 = pd.DataFrame(df3, columns = df2.columns.values)# データフレームに戻す
pca = PCA()# 主成分分析の準備
pca.fit(df3)# 主成分分析のモデルを作る
df4 = pd.DataFrame(pca.transform(df3), columns=["PC{}".format(x + 1) for x in range(len(df3.columns))])# 主成分を抽出
df5 = pd.concat([df11,df3, df4], axis = 1)# 元データと主成分の列を合体
df6 = pd.melt(df5, id_vars=['Y'])# データをグラフ用に並べ変える
sns.relplot(data=df6, x='value', y='Y', col='variable',kind='scatter',col_wrap = 3) # ひとつの量的変通と、他のすべての量的変数で散布図を描く
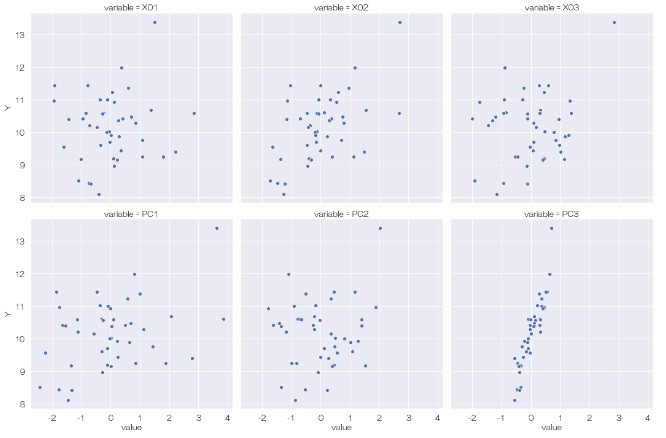
この結果を見ると、まず、Yと元のデータの他の変数(X01、X02、X03)には何も相関が見られないことがわかります。 次に、Yと主成分の関係を見ると、YとPC3には相関があることがわかります。 隠れ変数のようです。
この後ですが、隠れ変数が元の変数のどれに影響しているのかを調べます。
df7 = pd.DataFrame(pca.components_ ,columns = [df.columns],index = ["PC{}".format(x+1) for x in range(len(df.columns))])# 因子負荷量の抽出
sns.clustermap(df7, method='ward', metric='euclidean') # クラスタリング付きのヒートマップ
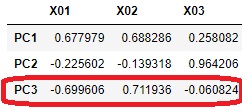
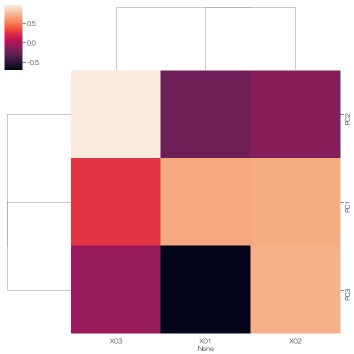
この結果を見ると、X03とPC3は、因子負荷量の絶対値が0に近いことから、隠れ変数のPC3は、X03には影響していないらしいことがわかりました。 PC3は、X01とX02に少し影響しているような因子のようです。
import os #パッケージの読み込み
import pandas as pd #パッケージの読み込み
import matplotlib.pyplot as plt# パッケージの読み込み
import seaborn as sns # パッケージの読み込み
from sklearn import preprocessing # パッケージの読み込み
from sklearn.decomposition import PCA# パッケージの読み込み
from sklearn.decomposition import FastICA# パッケージの読み込み
%matplotlib inline
sns.set(font='HGMaruGothicMPRO') # PandasのPlotのグラフの見た目をseaborn風にする。グラフのフォントを設定する
os.chdir("C:\\PyTest") # 作業用ディレクトリを変更
df= pd.read_csv("Data.csv" , engine='python')# データを読み込み
df11 =pd.DataFrame(df['Y'])# Yの列を別に作っておく
df12 = df.drop('Y', axis=1)# Y以外の列を別に作っておく
df2 = pd.get_dummies(df12)# 質的変数はダミー変換
df3 = preprocessing.scale(df2)# 正規化
df3 = pd.DataFrame(df3, columns = df2.columns.values)# データフレームに戻す
pca = PCA()# 主成分分析の準備
pca.fit(df3)# 主成分分析のモデルを作る
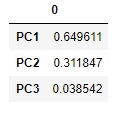
pd.DataFrame(pca.explained_variance_ratio_, index=["PC{}".format(x + 1) for x in range(len(df3.columns))])# 寄与率を抽出
ICA = FastICA(n_components=3, random_state=0)# 独立成分分析。成分は3つ抽出の場合
ICA.fit(df3)# 独立成分分析のモデルを作る
df4 = pd.DataFrame(ICA.transform(df3), columns=["IC{}".format(x + 1) for x in range(len(df3.columns))])# 主成分を抽出
df5 = pd.concat([df11,df3, df4], axis = 1)# 元データと主成分の列を合体
df6 = pd.melt(df5, id_vars=['Y'])# データをグラフ用に並べ変える
sns.relplot(data=df6, x='value', y='Y', col='variable',kind='scatter',col_wrap = 3) # ひとつの量的変通と、他のすべての量的変数で散布図を描く
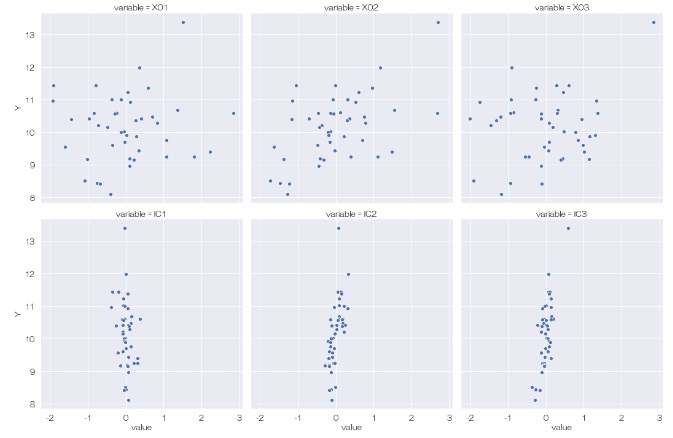
Yと独立成分の関係を見ると、隠れ変数はないように見えます。
この後ですが、隠れ変数が元の変数のどれに影響しているのかを調べたいのですが、 主成分分析の時のようなやり方を筆者がわからないです。 わかったらここに追記するつもりです。
import os #パッケージの読み込み
import pandas as pd #パッケージの読み込み
import matplotlib.pyplot as plt# パッケージの読み込み
import seaborn as sns # パッケージの読み込み
from sklearn import preprocessing # パッケージの読み込み
from sklearn.decomposition import PCA# パッケージの読み込み
%matplotlib inline
sns.set(font='HGMaruGothicMPRO') # PandasのPlotのグラフの見た目をseaborn風にする。グラフのフォントを設定する
os.chdir("C:\\PyTest") # 作業用ディレクトリを変更
df= pd.read_csv("Data.csv" , engine='python')# データを読み込み
df11 =pd.DataFrame(df['Y'])# Yの列を別に作っておく
df12 = df.drop('Y', axis=1)# Y以外の列を別に作っておく
df2 = pd.get_dummies(df12)# 質的変数はダミー変換
df3 = preprocessing.scale(df2)# 正規化
df3 = pd.DataFrame(df3, columns = df2.columns.values)# データフレームに戻す
pca = PCA()# 主成分分析の準備
pca.fit(df3)# 主成分分析のモデルを作る
df4 = pd.DataFrame(pca.transform(df3), columns=["PC{}".format(x + 1) for x in range(len(df3.columns))])# 主成分を抽出
df5 = pd.concat([df11,df3, df4], axis = 1)# 元データと主成分の列を合体
df6 = pd.melt(df5, id_vars=['Y'])# データをグラフ用に並べ変える
sns.boxplot(data=df6, x='variable', y='value', hue='Y') # 箱ひげ図
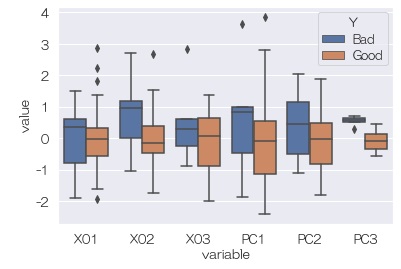
次に、Yと主成分の関係を見ると、PC3ではYがかなり明確に分離されます。 隠れ変数のようです。
隠れ変数が元の変数のどれに影響しているのかの調べ方は、注目している変数が量的変数の場合で主成分分析を使った時と同じです。
import os #パッケージの読み込み
import pandas as pd #パッケージの読み込み
import matplotlib.pyplot as plt# パッケージの読み込み
import seaborn as sns # パッケージの読み込み
from sklearn import preprocessing # パッケージの読み込み
from sklearn.decomposition import PCA# パッケージの読み込み
from sklearn.decomposition import FastICA# パッケージの読み込み
%matplotlib inline
sns.set(font='HGMaruGothicMPRO') # PandasのPlotのグラフの見た目をseaborn風にする。グラフのフォントを設定する
os.chdir("C:\\PyTest") # 作業用ディレクトリを変更
df= pd.read_csv("Data.csv" , engine='python')# データを読み込み
df11 =pd.DataFrame(df['Y'])# Yの列を別に作っておく
df12 = df.drop('Y', axis=1)# Y以外の列を別に作っておく
df2 = pd.get_dummies(df12)# 質的変数はダミー変換
df3 = preprocessing.scale(df2)# 正規化
df3 = pd.DataFrame(df3, columns = df2.columns.values)# データフレームに戻す
pca = PCA()# 主成分分析の準備
pca.fit(df3)# 主成分分析のモデルを作る
pd.DataFrame(pca.explained_variance_ratio_, index=["PC{}".format(x + 1) for x in range(len(df3.columns))])# 寄与率を抽出

ICA = FastICA(n_components=3, random_state=0)# 独立成分分析。成分は3つ抽出の場合
ICA.fit(df3)# 独立成分分析のモデルを作る
df4 = pd.DataFrame(ICA.transform(df3), columns=["IC{}".format(x + 1) for x in range(len(df3.columns))])# 主成分を抽出
df5 = pd.concat([df11,df3, df4], axis = 1)# 元データと主成分の列を合体
df6 = pd.melt(df5, id_vars=['Y'])# データをグラフ用に並べ変える
sns.boxplot(data=df6, x='variable', y='value', hue='Y') # 箱ひげ図
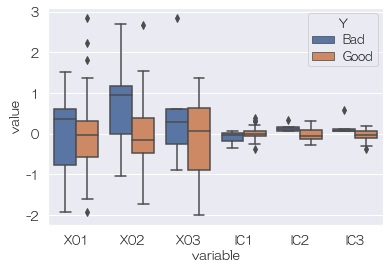
Yと独立成分の関係を見ると、隠れ変数はないように見えます。
主成分分析は、このページを参考にさせていただきました。
https://qiita.com/maskot1977/items/082557fcda78c4cdb41f
独立成分分析は、このページを参考にさせていただきました。
https://qiita.com/yuta-takahashi/items/c05908db9aebd1afa99f

