このページでは、 MAレスSARIMAXモデル をExcelで実施する手順を説明します。
モデルの係数は、分析ツールにある重回帰分析で簡単に求められます。
予測値は、 TREND関数 で簡単に求まります。
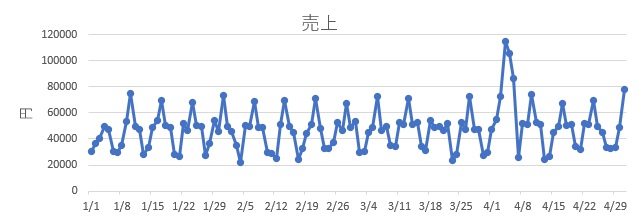
以下では、下のデータを分析します。 グラフは１月から４月ですが、１２月までの売上データを分析します。
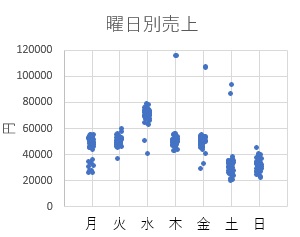
水曜日は売上が高めで、土日が低めです。 そのため、７日の周期を持っていることが事前にわかっています。
また、祝日は、平日だとしても、土日と同じくらいになります。
４月と10月に、３日間ずつセールをしていて、その時は非常に高くなります。
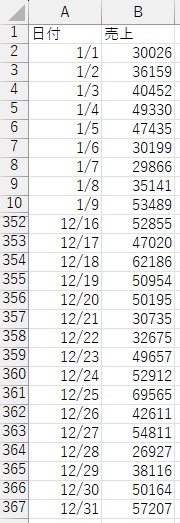
まず、データを用意します。
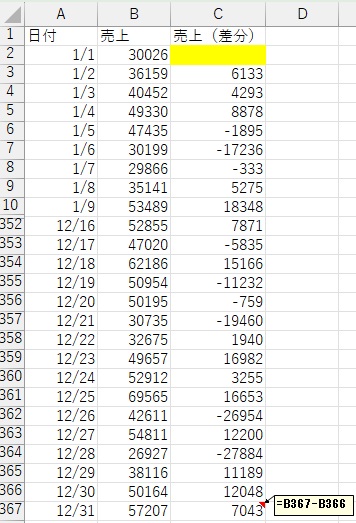
Iモデルにしたい場合は、下記のARやSの部分を作る前に、元のデータの差分データを作ります。 その差分データについて、ARやSの作業をすれば、Iモデルを作ったことになります。
この例ではIモデルは使いませんが、もしも差分データを作るのなら、以下のようになります。
ARモデルの部分については、元のデータを、１行ずらしたデータを作って、新しい変数にします。
必要に応じて、２行や３行ずらした変数も作ります。
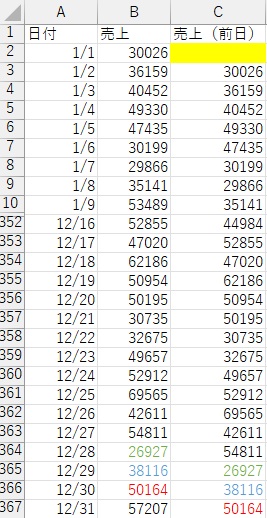
Sモデルの部分については、元のデータを、１周期分ずらしたデータを作って、新しい変数にします。
例えば、ここでは周期が７日なので、７日分ずらしたデータの変数を作ります。
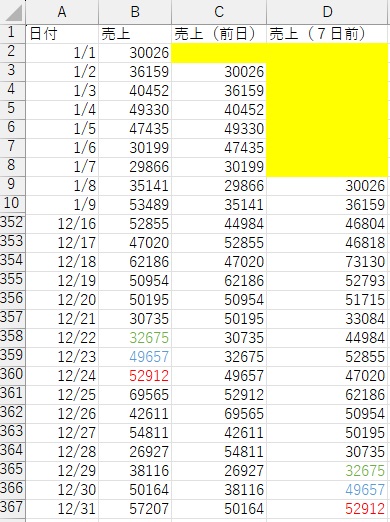
Xモデルの部分については、上記までで作ったテーブルデータの各行について、その時点での外生変数の値を充てて、新しい変数とします。 外生変数は、複数あれば、それらをそのまま複数の変数として扱います。
土日祝日だけ１にした変数と、セールの日だけ１にした変数を足します。
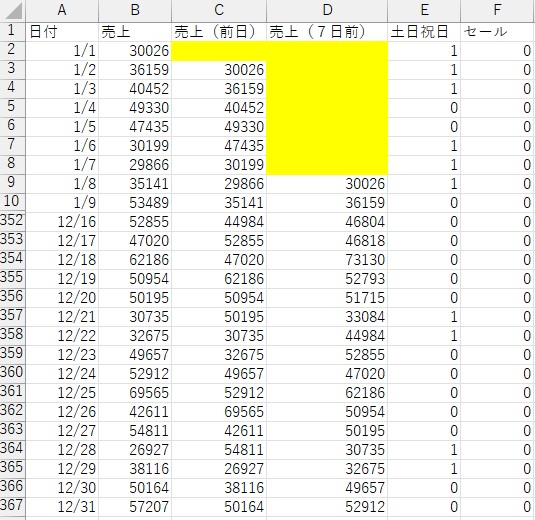
できたデータは、最初の７行の、1/1から1/7までは、欠損値があります。
欠損値がある行は、分析で使えないので、削除します。
なお、今回は削除しますが、
外れ値や欠損値のあるデータの解析
のページにあるように、どんな場合でも削除するとは限らないです。
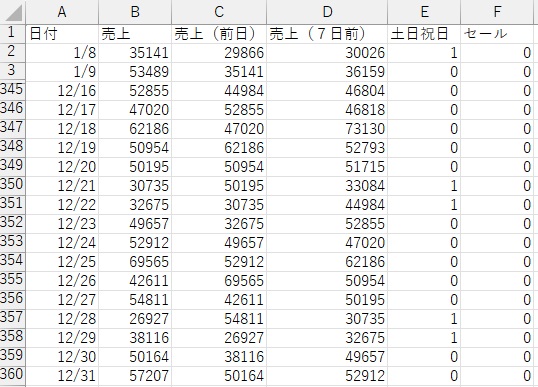
「データ」タブの、「データ分析」を選びます。
「回帰分析」を選びます。
データの範囲を入力します。
Yが元データで、Xが新しく作った変数です。
ラベルにもチェックを入れます。
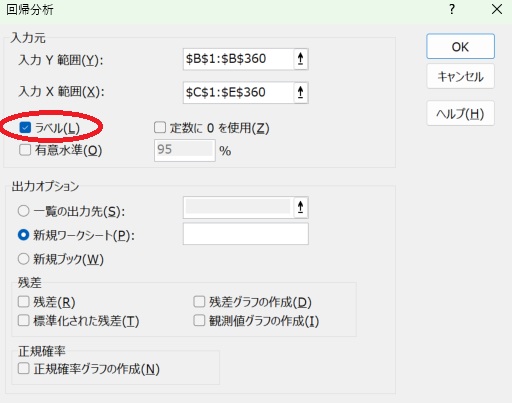
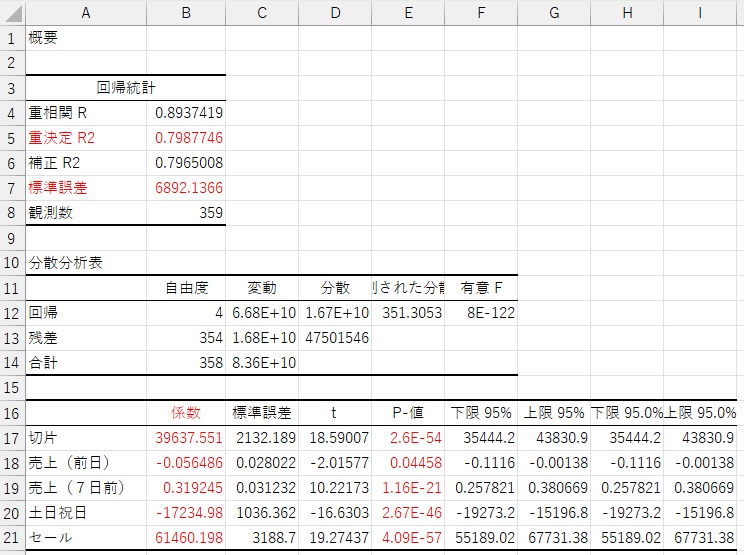
分析データが新しくできたシートに記入されます。
まず、重決定R2（相関係数Rの二乗：寄与率）が0.79…なので、高い精度があることがわかります。
精度については、標準誤差からもわかります。 予測区間 は、標準誤差の±約２倍の範囲が95％の予測区間になります。 標準誤差が約7000（6892…）となので、予測値を中心として、上下に約14000円ずつばらつきがあります。 そのため、これは、例えば、「予測値が50000円の場合、実際は36000円〜64000円にある可能性はあるが、その範囲より外は可能性が低い」ということがわかります。
変数が４つありますが、売上（前日）は、係数が小さく、P値が比較的大きいことから、無視しても良いようです。
当初の見立ての通り、それ以外の３つが支配的と考えて良さそうです。
12/31までのデータがあるので、次の年の1/1のデータを予測します。 1/1の予測をするには、説明変数のセルを埋めます。 1/1は、祝日なので、祝日の変数は１です。 また、セールはしないので、セールの変数は０です。
TREND関数で重回帰分析による予測ができます。
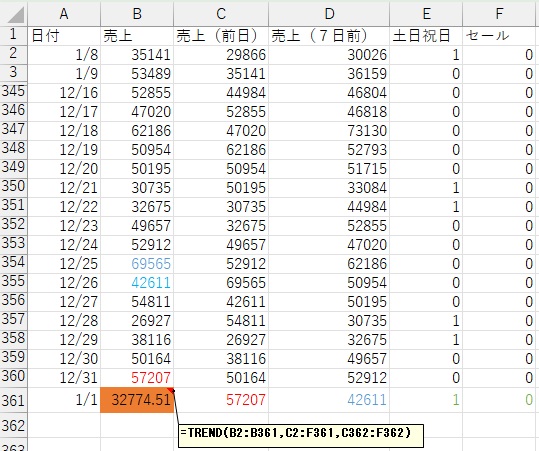
これで1/1の予測値が求まりました。 1/1の予測をする時に、前日の予測値を使いましたが、 1/2以降についても同様です。
TREND関数では、中心値が求まります。 予測区間は、中心値から上下に約14000円の範囲です。
