This is a method of analyzing the grouping of individual categories .
Basically, it is a method for qualitative variables, but quantitative variables are a one-dimensional clustering method and contain code to convert to qualitative variables, so qualitative and quantitative are mixed. , Only quantitative variables can be used.
For quantitative variables only, it can be used as a way to analyze the non-linear relationships of variables.
It is a method of combining correspondence analysis and multidimensional scaling .
library(dummies) #
library(MASS) #
library(ggplot2) #
setwd("C:/Rtest") #
Data <- read.csv("Data.csv", header=T) #
for (i in 1:ncol(Data)) { #
if (class(Data[,i]) == "numeric") {#
Data[,i] <- droplevels(cut(Data[,i], breaks = 5,include.lowest = TRUE))#
}#
}#
Data_dmy <- dummy.data.frame(Data)#
pc <- corresp(Data_dmy,nf=nf=min(ncol(Data),nrow(Data)))#
pc1 <- pc$cscore #
pc1 <- transform(pc1 ,name1 = rownames(pc1))#
round(pc$cor^2/sum(pc$cor^2),2)#
#In the above example, the 7th and subsequent eigenvalues ??have a low contribution rate, so we will exclude them from the subsequent analysis.
MaxN = 6#
Data11 <- pc1[,1:MaxN]#
Data11_dist <- dist(Data11)#
sn <- sammon(Data11_dist) #
output <- sn$points#
Data2 <- cbind(output, pc1)#
ggplot(Data2, aes(x=Data2[,1], y=Data2[,2],label=name1)) + geom_text() #
plot of words using Name Plots close to each other have a high degree of similarity. .. The vertical and horizontal axes of the graph have no particular meaning.
This is a method of combining association analysis and network graphs .
setwd("C:/Rtest") #
library(arules) #
library(dummies)#
library(igraph)#
library(ggplot2)#
Data <- read.csv("Data.csv", header=T) #
for (i in 1:ncol(Data)) { #
if (class(Data[,i]) == "numeric") { #
Data[,i] <- droplevels(cut(Data[,i], breaks = 5,include.lowest = TRUE))#
} #
} #
Data <- dummy.data.frame(Data)#
Data3 <- as(Data, "matrix")#
Data4 <- as(Data3, "transactions")#
ap <- apriori(Data4, parameter = list(support = 5/nrow(Data), maxlen = 2, minlen = 2))#
ap_inspect <- inspect(ap)#
ap_inspect$set <- paste(ap_inspect$lhs,"->",ap_inspect$rhs)#
# Process for drawing a bar graph
ap21 <- head(ap_inspect[order(ap_inspect$support, decreasing=T),],20)#
ggplot(ap21, aes(x=support, y=reorder(set, support))) + geom_bar(stat = "identity") #
ap22 <- head(ap_inspect[order(ap_inspect$confidence, decreasing=T),],20)#
ggplot(ap22, aes(x=confidence, y=reorder(set, confidence))) + geom_bar(stat = "identity") #
ap23 <- head(ap_inspect[order(ap_inspect$lift, decreasing=T),],20)#
ggplot(ap23, aes(x=lift, y=reorder(set, lift))) + geom_bar(stat = "identity")#
#network graph
ap31<- graph.data.frame(ap21[,c(1,3)], directed = F)#
plot(ap31)#
ap32<- graph.data.frame(ap22[,c(1,3)])#
plot(ap32)#
ap33<- graph.data.frame(ap23[,c(1,3)])#
plot(ap33)#
below are all confidence graphs.
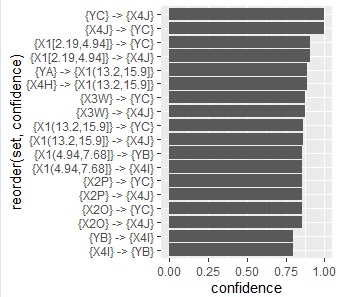
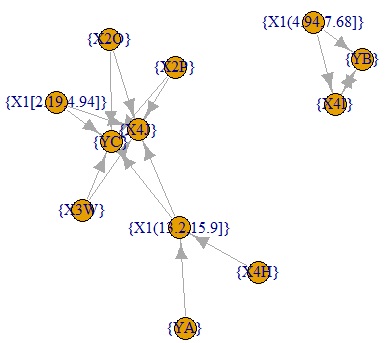
The arrows only represent the inclusion relationship of the data, not the causal relationship. ( This story is summarized in detail in the relationship between if-then rules and causality .)
In the above code, I set the parameters according to the following idea. I don't know if it's the best.
