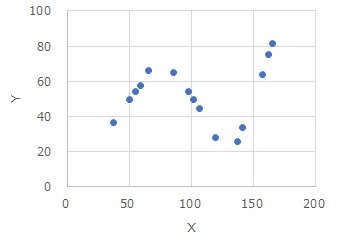
区間高次元化回帰分析 のRによる実施例です。
この実施例は、
区間高次元化回帰分析
のページと、ほぼ同じ手順をRで実行しています。
Rによる一般化線形混合モデル にあるような一般化線形混合モデルや、交互作用モデルを使うと、コードはシンプルにする方法もあります。 しかし、この方法を使うと、xの元データの項がモデルに入って来て、係数の評価がわかりにくくなります。
library(MASS)
library(fastDummies)# ライブラリを読み込み
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
Data1 <- Data
DataY <- Data
DataY$X <- NULL
Data1$Y <- NULL
DataX <- Data1
for (i in 1:ncol(Data1)) {1
Data1[,i] <- droplevels(cut(Data1[,i], breaks = 3,include.lowest = TRUE))# 1列目の量的変数を１次元クラスタリングで３つカテゴリに分ける
}
Data2 <- dummy_cols(Data1,remove_first_dummy = FALSE,remove_selected_columns = TRUE)# ダミー変換
Data3 <-Data2*DataX[,1]# 交互作用項の作成
colnames(Data3)<-paste0("X:",colnames(Data3))# 変数名の修正
Data4 <-cbind(DataY,Data2,Data3)
gm <- step(glm(Y~., data=Data4, family= gaussian(link = "identity"))) # 重回帰分析
summary(gm) # 結果の出力
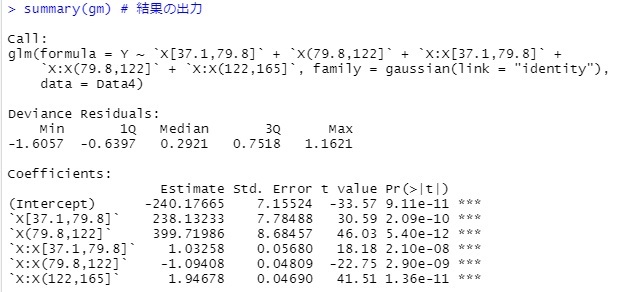
#ここから予測の手順
library(ggplot2)
s2 <- predict(gm,Data4)# 作業用ディレクトリを変更
Data4s2 <- cbind(Data4,s2)# データを読み込み
ggplot(Data4s2, aes(x=Y, y=s2)) + geom_point() + labs(x="Y",y="predicted Y")
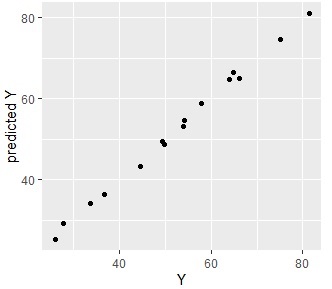
上の実施例は、元のYと、予測値のYを比べて、モデルの出来栄えを確認しています。
Rによるベクトル量子化回帰分析 では、この後に、任意の位置についての予測値を出すためのコードもあります。
このページの区間高次元化回帰分析では、任意の位置の予測値は、入力データの作り方がよくわからないこともあり、入れていません。 ただ、 区間高次元化回帰分析 は、 ベクトル量子化回帰分析 よりも、モデルの 説明可能性・解釈可能性 が良いので、使い分けると良いように考えています。 探索的なデータ分析の時は、区間高次元化回帰分析が良いです。 ブラックボックスでも良いので精度の高い機械学習モデルが欲しい時は、ベクトル量子化回帰分析が良いです。
